练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    每个正整数都可以表示成一个或者多个连续正整数的和．试对每个正整数n，求n有多少种不同的方法表示成这样的和．

    解析：设m为n的正的奇因数，m＝nd，则

    若(1)的每一项都是正的，则它就是n的一种表示(表成连续正整数的和)．

    若(1)式右边有负数与0，则这些负数与它们的相反数抵消(因

    以略去，这样剩下的项是连续的正整数，仍然得到n的一种表示，其项数为偶数(例如7＝(－2)＋(－1)＋0＋1＋2＋3＋4＝3＋4)

    于是n的每一个正奇因数产生一个表示．

    反过来，若n有一个表示，项数为奇数m，则它就是(1)的形式，而m是n的奇因数，若n有一个表示，项数为偶数，最小一项为k＋1，则可将这表示向负的方向“延长”，增加2k＋1项，这些项中有0及±1，±2，…，±k．这样仍成为(1)的形式，项数是n的奇因数．

    因此，n的表示法正好是n的正奇因数的个数，如果n的标准分解

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

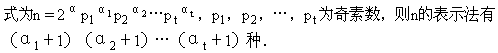
    科目：高中数学 来源： 题型：

    对于每个正整数n，以s(n)表示满足如下条件的最大正整数：对于每个正整数k≤s(n)，n2都可以表示成k个正整数的平方之和．

    1．证明：对于每个正整数n≥4，都有s(n)≤n2－14；

    2．试找出一个正整数n，使得s(n)＝n2－14；

    3．证明：存在无限多个正整数n，使得s(n)＝n2－14．

    查看答案和解析>>

    同步练习册答案