
【题目】已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧, ![]()
![]() =2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
【答案】B
【解析】解:设直线AB的方程为:x=ty+m,点A(x1 , y1),B(x2 , y2), 直线AB与x轴的交点为M(m,0),
由 ![]() y2﹣ty﹣m=0,根据韦达定理有y1y2=﹣m,
y2﹣ty﹣m=0,根据韦达定理有y1y2=﹣m,
∵ ![]()
![]() =2,∴x1x2+y1y2=2,
=2,∴x1x2+y1y2=2,
结合 ![]() 及
及 ![]() ,得
,得 ![]() ,
,
∵点A,B位于x轴的两侧,∴y1y2=﹣2,故m=2.
不妨令点A在x轴上方,则y1>0,又 ![]() ,
,
∴S△ABO+S△AFO═ ![]() ×2×(y1﹣y2)+
×2×(y1﹣y2)+ ![]() ×
× ![]() y1 ,
y1 ,
= ![]() .
.
当且仅当 ![]() ,即
,即 ![]() 时,取“=”号,
时,取“=”号,
∴△ABO与△AFO面积之和的最小值是3,故选B.
可先设直线方程和点的坐标,联立直线与抛物线的方程得到一个一元二次方程,再利用韦达定理及 ![]()
![]() =2消元,最后将面积之和表示出来,探求最值问题.
=2消元,最后将面积之和表示出来,探求最值问题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}满足a1+a2+…+an+2n= ![]() (an+1+1),n∈N* , 且a1=1,求证:
(an+1+1),n∈N* , 且a1=1,求证:
(1)数列{an+2n}是等比数列;
(2)求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值t构成的集合是( ) 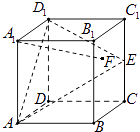
A.{t| ![]() }
}
B.{t| ![]() ≤t≤2}
≤t≤2}
C.{t|2 ![]() }
}
D.{t|2 ![]() }
}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一批产品的长度(单位:mm)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.用频率估计概率,现从该批产品中随机抽取一件,则其为二等品的概率为( ) 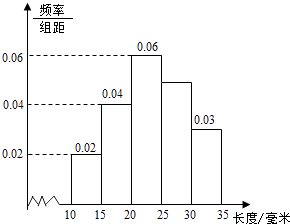
A.0.09
B.0.20
C.0.25
D.0.45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱柱(底面是正三角形的直棱柱)ABC﹣A1B1C1中,已知AB=2,CC1= ![]() ,则异面直线AB1和BC1所成角的正弦值为( )
,则异面直线AB1和BC1所成角的正弦值为( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: ①平面A′FG⊥平面ABC;
②BC∥平面A′DE;
③三棱锥A′﹣DEF的体积最大值为 ![]() a3;
a3;
④动点A′在平面ABC上的射影在线段AF上;
⑤二面角A′﹣DE﹣F大小的范围是[0, ![]() ].
].
其中正确的命题是(写出所有正确命题的编号)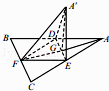
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() +
+ ![]() =1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,且|AB|=
=1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,且|AB|= ![]() |BF|.
|BF|. 
(Ⅰ)求椭圆C的离心率;
(Ⅱ)若斜率为2的直线l过点(0,2),且l交椭圆C于P、Q两点,OP⊥OQ.求直线l的方程及椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),0<β<α<π.
=(cosβ,sinβ),0<β<α<π.
(1)若| ![]() ﹣
﹣ ![]() |=
|= ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() ;
;
(2)设c=(0,1),若 ![]() +
+ ![]() =c,求α,β的值.
=c,求α,β的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() ,
, ![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ![]() =(﹣
=(﹣ ![]() ,1).
,1).
(1)若| ![]() |=2 且
|=2 且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标;
的坐标;
(2)若| ![]() |=
|= ![]() ,(
,( ![]() +3
+3 ![]() )⊥(
)⊥( ![]() ﹣
﹣ ![]() ),求向量
),求向量 ![]() ,
, ![]() 的夹角的余弦值.
的夹角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com