Question

【题目】已知 ， ， 是同一平面内的三个向量，其中 =（﹣ ，1）．
（1）若| |=2 且 ∥ ，求 的坐标；
（2）若| |= ，（ +3 ）⊥（ ﹣ ），求向量 ， 的夹角的余弦值．

Answer 1

【答案】
（1）解：设 =（m，n），

若| |=2 且 ∥ ，其中 =（﹣ ，1），

可得m2+n2=4，m=﹣ n，

解得m=﹣ ，n= 或m= ，n=﹣ ，

则 =（﹣ ， ）或（ ，﹣ ）

（2）解：若 =（﹣ ，1），可得| |= ，

又| |= ，（ +3 ）⊥（ ﹣ ），

可得（ +3 ）（ ﹣ ）= 2﹣3 2+2 =0，

即有3﹣3×2+2 =0，

可得 = ，

向量 ， 的夹角的余弦值为 = =

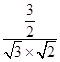【解析】（1）设 =（m，n），运用向量模的公式和向量共线的坐标表示，解方程即可得到所求；（2）由向量垂直的条件：数量积为0，以及向量的平方即为模的平方，化简整理，可得 = ，再由向量夹角的余弦公式，计算即可得到所求值．