
【题目】记所有非零向量构成的集合为V,对于 ![]() ,
, ![]() ∈V,
∈V, ![]() ≠
≠ ![]() ,定义V(
,定义V( ![]() ,
, ![]() )=|x∈V|x
)=|x∈V|x ![]() =x
=x ![]() |
|
(1)请你任意写出两个平面向量 ![]() ,
, ![]() ,并写出集合V(
,并写出集合V( ![]() ,
, ![]() )中的三个元素;
)中的三个元素;
(2)请根据你在(1)中写出的三个元素,猜想集合V( ![]() ,
, ![]() )中元素的关系,并试着给出证明;
)中元素的关系,并试着给出证明;
(3)若V( ![]() ,
, ![]() )=V(
)=V( ![]() ,
, ![]() ),其中
),其中 ![]() ≠
≠ ![]() ,求证:一定存在实数λ1 , λ2 , 且λ1+λ2=1,使得
,求证:一定存在实数λ1 , λ2 , 且λ1+λ2=1,使得 ![]() =λ1
=λ1 ![]() +λ2
+λ2 ![]() .
.
【答案】
(1)解:比如 ![]() =(1,2),
=(1,2), ![]() =(3,4),设
=(3,4),设 ![]() =(x,y),
=(x,y),
由 ![]()
![]() =
= ![]()
![]() ,可得x+2y=3x+4y,
,可得x+2y=3x+4y,
即为x+y=0,
则集合V( ![]() ,
, ![]() )中的三个元素为(1,﹣1),(2,﹣2),(3,﹣3);
)中的三个元素为(1,﹣1),(2,﹣2),(3,﹣3);
(2)解:由(1)可得这些向量共线.
理由:设 ![]() =(s,t),
=(s,t), ![]() =(a,b),
=(a,b), ![]() =(c,d),
=(c,d),
由 ![]()
![]() =
= ![]()
![]() ,可得as+bt=cs+dt,
,可得as+bt=cs+dt,
即有s= ![]() t,
t,
即 ![]() =(
=( ![]() t,t),
t,t),
故集合V( ![]() ,
, ![]() )中元素的关系为共线;
)中元素的关系为共线;
(3)证明:设 ![]() =(s,t),
=(s,t), ![]() =(a,b),
=(a,b), ![]() =(c,d),
=(c,d),
![]() =(u,v),
=(u,v), ![]() =(e,f),
=(e,f),
若V( ![]() ,
, ![]() )=V(
)=V( ![]() ,
, ![]() ),
),
即有as+bt=cs+dt,au+bv=ue+fv,
解得a= ![]() c+
c+ ![]() e+
e+ ![]() ,
,
可令d=f,可得λ1= ![]() ,
,
λ2= ![]() ,
,
则一定存在实数λ1,λ2,且λ1+λ2=1,使得 ![]() =λ1
=λ1![]() +λ2
+λ2![]() .
.
【解析】(1)比如 ![]() =(1,2),
=(1,2), ![]() =(3,4),设
=(3,4),设 ![]() =(x,y),运用数量积的坐标表示,即可得到所求元素;(2)由(1)可得这些向量共线.理由:设
=(x,y),运用数量积的坐标表示,即可得到所求元素;(2)由(1)可得这些向量共线.理由:设 ![]() =(s,t),
=(s,t), ![]() =(a,b),
=(a,b), ![]() =(c,d),运用数量积的坐标表示,以及共线定理即可得到;(3)设
=(c,d),运用数量积的坐标表示,以及共线定理即可得到;(3)设 ![]() =(s,t),
=(s,t), ![]() =(a,b),
=(a,b), ![]() =(c,d),
=(c,d), ![]() =(u,v),
=(u,v), ![]() =(e,f),运用新定义和数量积的坐标表示,解方程可得a,即可得证.
=(e,f),运用新定义和数量积的坐标表示,解方程可得a,即可得证.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() +
+ ![]() =1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,且|AB|=
=1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,且|AB|= ![]() |BF|.
|BF|. 
(Ⅰ)求椭圆C的离心率;
(Ⅱ)若斜率为2的直线l过点(0,2),且l交椭圆C于P、Q两点,OP⊥OQ.求直线l的方程及椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥底面ABCD,M是棱PC上一点.若PA=AC=a,则当△MBD的面积为最小值时,直线AC与平面MBD所成的角为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() ,
, ![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ![]() =(﹣
=(﹣ ![]() ,1).
,1).
(1)若| ![]() |=2 且
|=2 且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标;
的坐标;
(2)若| ![]() |=
|= ![]() ,(
,( ![]() +3
+3 ![]() )⊥(
)⊥( ![]() ﹣
﹣ ![]() ),求向量
),求向量 ![]() ,
, ![]() 的夹角的余弦值.
的夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 其中M∪P=R,则下列结论中一定正确的是( )
其中M∪P=R,则下列结论中一定正确的是( )
A.函数f(x)一定存在最大值
B.函数f(x)一定存在最小值
C.函数f(x)一定不存在最大值
D.函数f(x)一定不存在最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF= ![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( ) 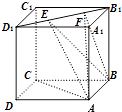
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A﹣BEF的体积为定值
D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1+x)﹣loga(1﹣x)(a>0且a≠1),
(1)求函数f(x)的定义域;
(2)若关于x的方程|f(x)|=2的解集为 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(﹣2,1).
(1)当直线l与点B(﹣5,4)、C(3,2)的距离相等时,求直线l的方程;
(2)当直线l与x轴、y轴围成的三角形的面积为 ![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com