
已知函数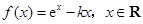
(Ⅰ)若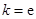 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(Ⅱ)若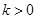 ,且对于任意
,且对于任意 ,
, 恒成立,试确定实数
恒成立,试确定实数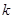 的取值范围;
的取值范围;
(Ⅲ)设函数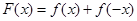 ,求证:
,求证: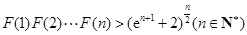 .
.
(1)增区间是 ,减区间是
,减区间是
(2)
(3)构造函数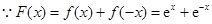 ,
,

 ,
,
则放缩法得到证明。
【解析】
试题分析:解:(Ⅰ)由 得
得 ,所以
,所以 .
.
由 得
得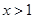 ,故
,故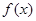 的单调递增区间是
的单调递增区间是 ,
,
由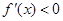 得
得 ,故
,故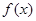 的单调递减区间是
的单调递减区间是 .
.
(Ⅱ)由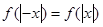 可知
可知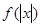 是偶函数.
是偶函数.
于是 对任意
对任意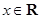 成立等价于
成立等价于 对任意
对任意 成立.
成立.
由 得
得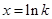 .
.
①当 时,
时,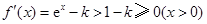 .
.
此时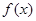 在
在 上单调递增.故
上单调递增.故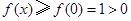 ,符合题意.
,符合题意.
②当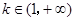 时,
时, .
.
当 变化时
变化时 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
单调递减 |
极小值 |
单调递增 |
由此可得,在 上,
上, .
.
依题意, ,又
,又 .
.
综合①,②得,实数 的取值范围是
的取值范围是 .
.
(Ⅲ)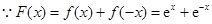 ,
,

 ,
,
 ,
,
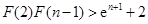
…….

由此得,
故 .
.
考点:导数的运用
点评:解决的关键是对于函数单调性的判定以及运用函数的极值来得到参数的 范围,属于中档题。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014届广东省韶关市高三摸底测试理科数学试卷(解析版) 题型:解答题
已知函数 ,
, 
 .
.
(1)若 , 函数
, 函数 在其定义域是增函数,求
在其定义域是增函数,求 的取值范围;
的取值范围;
(2)在(1)的结论下,设函数 的最小值;
的最小值;
(3)设函数 的图象
的图象 与函数
与函数 的图象
的图象 交于点
交于点 ,过线段
,过线段 的中点
的中点 作
作 轴的垂线分别交
轴的垂线分别交 、
、 于点
于点 、
、 ,问是否存在点
,问是否存在点 ,使
,使 在
在 处的切线与
处的切线与 在
在 处的切线平行?若存在,求出
处的切线平行?若存在,求出 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省金华十校高三上学期期末考试理科数学(解析版) 题型:解答题
(本题满分16分)
已知函数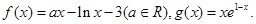
(1)若函数 图象在(0,0)处的切线也恰为
图象在(0,0)处的切线也恰为 图象的一条切线,求实数a的值;
图象的一条切线,求实数a的值;
(2)是否存在实数a,对任意的 ,都有唯一的
,都有唯一的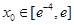 ,使得
,使得 成立,若存在,求出a的取值范围;若不存在,请说明理由。
成立,若存在,求出a的取值范围;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省福州市高三年级第二次月考数学试题(理科) 题型:解答题
(本小题满分14分)
已知函数
(1)若 ,求
,求 的单调递减区间;
的单调递减区间;
(2)若 ,求
,求 的最小值;
的最小值;
(3)若 ,且存在
,且存在 使得
使得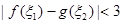 ,求实数
,求实数 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2013届浙江省宁波市高一上学期期末数学卷 题型:解答题
(本小题满分15分)
已知函数 .
.
(1)若 ,求函数
,求函数 在区间
在区间 的值域;
的值域;
(2)若函数 在
在 上为增函数,求
上为增函数,求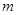 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com