
已知平面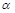 ∥
∥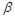 ,直线l
,直线l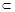
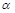 ,点P∈l,平面
,点P∈l,平面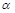 、
、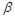 间的距离为5,则在
间的距离为5,则在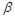 内到点P的距离为13且到直线l的距离为
内到点P的距离为13且到直线l的距离为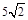 的点的轨迹是( )
的点的轨迹是( )
| A.一个圆 | B.四个点 | C.两条直线 | D.双曲线的一支 |
B
解析考点:抛物线的定义.
专题:计算题.
分析:如图所示:作PH⊥β,H为垂足,过H 作直线m∥l,则m是l在平面β内的摄影.作HA⊥m,且HA=PH=5,则由三垂线定理可得 PA⊥l,作AM∥m,且 AM= 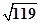 ,有勾股定理可得MP=13,故M在所求的轨迹上.据点M在面β内,可得满足条件的M共有4个.
,有勾股定理可得MP=13,故M在所求的轨迹上.据点M在面β内,可得满足条件的M共有4个.
解答: 解:如图所示:作PH⊥β,H为垂足,则PH=5.
解:如图所示:作PH⊥β,H为垂足,则PH=5.
过H 作直线m∥l,则m是l在平面β内的摄影.
作HA⊥m,且HA=PH=5,
则由三垂线定理可得 PA⊥m,∴PA⊥l,故 PA=5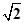 .
.
作AM∥m,且 AM=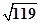 ,有勾股定理可得MP=13,故M在所求的轨迹上.又点M在面β内,
,有勾股定理可得MP=13,故M在所求的轨迹上.又点M在面β内,
故满足条件的M共有4个,
故选 B.
点评:本题考查勾股定理、三垂线定理的应用,体现了数形结合的数学思想,确定点M的位置,是解题的难点和关键.


科目:高中数学 来源: 题型:单选题
过抛物线 y2 =" 4x" 的焦点作直线交抛物线于A(x1, y1)B(x2, y2)两点,如果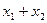 =6,
=6,
那么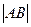 =( )
=( )
| A. 6 | B. 8 | C.9 | D.10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com