
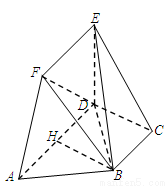
如图,在五面体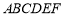 中,已知
中,已知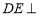 平面
平面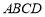 ,
,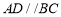 ,
,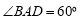 ,
,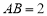 ,
,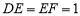 .
.
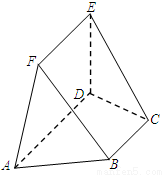
(1)求证: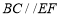 ;
;
(2)求三棱锥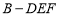 的体积.
的体积.
(1)详见解析,(2)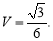
【解析】
试题分析:(1)证明线线平行,一般思路为利用线面平行的性质定理与判定定理进行转化. 因为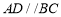 ,
,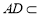 平面
平面 ,
,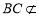 平面
平面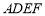 ,所以
,所以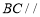 平面
平面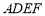 ,又
,又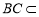 平面
平面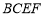 ,平面
,平面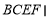 平面
平面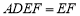 ,所以
,所以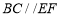 .(2)求三棱锥的体积,关键是找寻高.可由面面垂直性质定理探求,因为
.(2)求三棱锥的体积,关键是找寻高.可由面面垂直性质定理探求,因为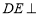 平面
平面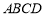 ,所以有面
,所以有面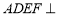 平面
平面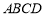 ,则作
,则作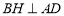 就可得
就可得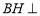 平面
平面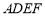 .证明
.证明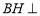 平面
平面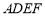 过程也可从线线垂直证线面垂直.确定
过程也可从线线垂直证线面垂直.确定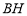 是三棱锥
是三棱锥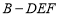 的高之后,可利用三棱锥
的高之后,可利用三棱锥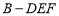 的体积公式
的体积公式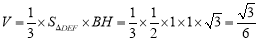 .
.
试题解析:
(1)因为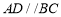 ,
,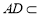 平面
平面 ,
,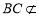 平面
平面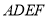 ,
,
所以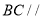 平面
平面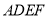 , 3分
, 3分
又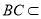 平面
平面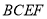 ,平面
,平面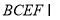 平面
平面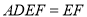 ,
,
所以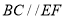 . 6分
. 6分
(2)在平面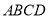 内作
内作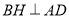 于点
于点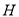 ,
,
因为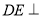 平面
平面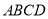 ,
,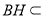 平面
平面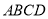 ,所以
,所以 ,
,
又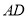 ,
,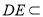 平面
平面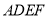 ,
,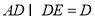 ,
,
所以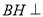 平面
平面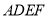 ,
,
所以 是三棱锥
是三棱锥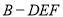 的高. 9分
的高. 9分
在直角三角形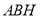 中,
中,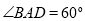 ,
,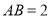 ,所以
,所以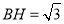 ,
,
因为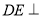 平面
平面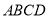 ,
,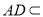 平面
平面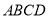 ,所以
,所以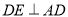 ,
,
又由(1)知,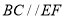 ,且
,且 ,所以
,所以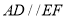 ,所以
,所以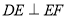 , 12分
, 12分
所以三棱锥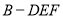 的体积
的体积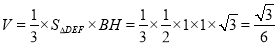 . 14分
. 14分
考点:线面平行判定定理与性质定理,线面垂直判定定理与性质定理,三棱锥体积


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2013-2014学年江苏省高三下学期4月周练文科数学试卷(解析版) 题型:填空题
为了检查某超市货架上的奶粉是否含有三聚氰胺,要从编号依次为01到50的袋装奶粉中抽取5袋进行检验,现将50袋奶粉按编号顺序平均分成5组,用每组选取的号码间隔一样的系统抽样方法确定所选取的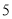 袋奶粉的编号,若第4组抽出的号码为36,则第1组中用抽签的方法确定的号码是 .
袋奶粉的编号,若第4组抽出的号码为36,则第1组中用抽签的方法确定的号码是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省徐州市高三第三次质量检测理科数学试卷(解析版) 题型:填空题
从高三年级随机抽取100名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为 .
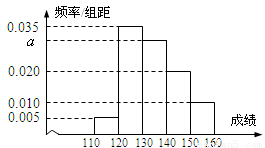
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省徐州市高三第三次质量检测文科数学试卷(解析版) 题型:填空题
从高三年级随机抽取100名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为 .
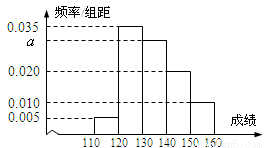
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高考模拟考试理科数学试卷(解析版) 题型:填空题
已知等差数列{an}的公差不为零,a1+a2+a5>13,且a1,a2,a5 成等比数列,则a1 的取值范围为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com