已知f(x)＝2＋log3x，x∈[1，9]，求y＝[f(x)]2＋f(x2)的最大值及y取最大值时x的值．
|
思路分析：要求函数y＝[f(x)]2＋f(x2)的最大值，要做两件事，一是要求其表达式；二是要求出它的定义域，然后求值域． 解：∵f(x)＝2＋log3x， ∴y＝[f(x)]2＋f(x2)＝(2＋log3x)2＋2＋log ＝(2＋log3x)2＋2＋2log3x ＝log32x＋6log3x＋6 ＝(log3x＋3)2－3． ∵函数f(x)的定义域为[1，9]， ∴要使函数y＝[f(x)]2＋f(x2)有定义，就需 ∴1≤x≤3．∴0≤log3x≤1． ∴6≤y＝(log3x＋3)2－3≤13． ∴当x＝3时，函数y＝[f(x)]2＋f(x2)取最大值13． 说明：本例正确求解的关键是：函数y＝[f(x)]2＋f(x2)定义域的正确确定．如果我们误认为[1，9]是它的定义域，则将求得错误的最大值22． 其实我们还能求出函数y＝[f(x)]2＋f(x2)的值域为[6，13]． |
科目：高中数学 来源：湖南省长沙市一中2010届高三上学期第二次月考(数学理) 题型：022
已知函数f(x)＝
，直线l：9x＋2y＋c＝0，当x∈[－2，2]时，函数y＝f(x)图象恒在直线l的下方，则c的取值范围是________．
查看答案和解析>>
科目：高中数学 来源：重庆市重庆一中2012届高三9月月考数学理科试题 题型：044
若存在实数k和b，使得函数f(x)与g(x)对其定义域上的任意实数x分别满足：f(x)≥kx＋b和g(x)≤kx＋b，则称直线l：y＝kx＋b为f(x)与g(x)的“和谐直线”．已知h(x)＝x2，
(x)＝2elnx，(e为自然对数的底数)；
(1)
求F(x)＝h(x)－(x)的极值；
(
2)函数h(x)和(x)是否存在和谐直线？若存在，求出此和谐直线方程；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源：2012年陕西省高二下期第一次月考理科数学试卷（解析版） 题型：解答题
已知函数f(x)＝x3－3x及y＝f(x)上一点P(1，－2)，过点P作直线l.
(1)求使直线l和y＝f(x)相切且以P为切点的直线方程；
(2)求使直线l和y＝f(x)相切且切点异于P的直线方程．
查看答案和解析>>
科目：高中数学 来源：新课标高三数学导数专项训练（河北） 题型：解答题
已知函数f(x)＝x3－2x2＋ax(x∈R，a∈R)，在曲线y＝f(x)的所有切线中，有且仅有一条切线l与直线y＝x垂直．
(1)求a的值和切线l的方程；
(2)设曲线y＝f(x)上任一点处的切线的倾斜角为θ，求θ的取值范围
查看答案和解析>>
科目：高中数学 来源：2010-2011学年甘肃省天水市高三第六次检测数学文卷 题型：解答题
（12分）已知动点P到定点F (
, 0 ) 的距离与点 P 到定直线 l：x＝2 的距离之比为
。
（1）求动点P的轨迹C的方程；
（2）设M、N是直线l上的两个点，点E是点F关于原点的对称点，若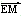
·
＝0，
求 | MN | 的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
