
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)①求函数![]() 的单调区间;
的单调区间;
②若![]() 满足
满足![]() ,且
,且![]() .求证:
.求证:![]() .
.
(2)函数![]() .若
.若![]() 对任意,
对任意,![]() 都有
都有![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)①单调递增区间![]() ,
,![]() ,单调递减区间
,单调递减区间![]() ;②详见解析;(2)
;②详见解析;(2)![]() .
.
【解析】
(1)①求导可得![]() ,再分别求解
,再分别求解![]() 与
与![]() 的解集,结合定义域分析函数的单调区间即可.
的解集,结合定义域分析函数的单调区间即可.
②根据(1)中的结论,求出![]() 的表达式,再分
的表达式,再分![]() 与
与![]() 两种情况,结合函数的单调性分析
两种情况,结合函数的单调性分析![]() 的范围即可.
的范围即可.
(2)求导分析![]() 的单调性,再结合
的单调性,再结合![]() 单调性,设
单调性,设![]() 去绝对值化简可得
去绝对值化简可得![]() ,再构造函数
,再构造函数![]() ,
,![]() ,根据函数的单调性与恒成立问题可知
,根据函数的单调性与恒成立问题可知![]() ,再换元表达
,再换元表达![]() 求解最大值即可.
求解最大值即可.
解:![]() ,
,
由![]() 可得
可得![]() 或
或![]() ,
,
由![]() 可得
可得![]() ,
,
故函数的单调递增区间![]() ,
,![]() ,单调递减区间
,单调递减区间![]() ;
;
![]() ,
,
![]() 或
或![]() ,
,
若![]() ,因为
,因为![]() ,故
,故![]() ,
,![]() ,
,
由![]() 知
知![]() 在
在![]() 上单调递增,
上单调递增,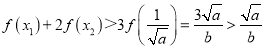 ,
,
若![]() 由
由![]() 可得
可得![]() x1,
x1,
因为![]() ,
,
所以![]() ,
,
由![]() 在
在![]() 上单调递增,
上单调递增,
![]()
综上![]() .
.
![]()
![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
不妨设![]()
由(1)![]() 在
在![]() 上单调递减,
上单调递减,
由![]() ,
,
可得![]() ,
,
所以![]() ,
,
令![]() ,
,![]() ,
,
可得![]() 单调递减,
单调递减,
所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,即
上恒成立,即![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() 的最大值
的最大值![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]() ,如图,曲线
,如图,曲线![]() 由曲线
由曲线![]() :
:![]() 和曲线
和曲线![]() :
:![]() 组成,其中点
组成,其中点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点,点
所在圆锥曲线的焦点,点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点.
所在圆锥曲线的焦点.
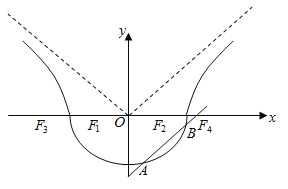
(Ⅰ)若![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(Ⅱ)如图,作直线![]() 平行于曲线
平行于曲线![]() 的渐近线,交曲线
的渐近线,交曲线![]() 于点
于点![]() ,求证:弦
,求证:弦![]() 的中点
的中点![]() 必在曲线
必在曲线![]() 的另一条渐近线上;
的另一条渐近线上;
(Ⅲ)对于(Ⅰ)中的曲线![]() ,若直线
,若直线![]() 过点
过点![]() 交曲线
交曲线![]() 于点
于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1+a2+…+an=an+1﹣2.
(1)若a1=2,求数列{an}的通项公式;
(2)若数列1,a2,a4,b1,b2,…bn,…成等差数列,求数列{bn}的前n项和为Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高一高二各班体育节的表现情况,统计了高一高二各班的得分情况并绘成如图所示的茎叶图,则下列说法正确的是( )
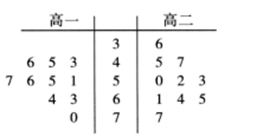
A.高一年级得分中位数小于高二年级得分中位数
B.高一年级得分方差大于高二年级得分方差
C.高一年级得分平均数等于高二年级得分平均数
D.高一年级班级得分最低为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】保护环境就是保护人类健康.空气中负离子浓度(单位:个/![]() )可以作为衡量空气质量的一个指标,也对人的健康有一定的影响.根据我国部分省市区气象部门公布的数据,目前对空气负离子浓度的等级标准如下表
)可以作为衡量空气质量的一个指标,也对人的健康有一定的影响.根据我国部分省市区气象部门公布的数据,目前对空气负离子浓度的等级标准如下表![]() .
.
表![]() 负离子浓度与空气质量对应标准:
负离子浓度与空气质量对应标准:
负离子浓度 | 等级 | 和健康的关系 |
|
| 不利 |
|
| 正常 |
|
| 较有利 |
|
| 有利 |
|
| 相当有利 |
|
| 很有利 |
|
| 极有利 |
图![]() 空气负离子浓度
空气负离子浓度
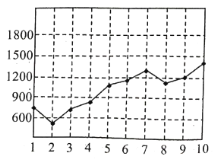
某地连续![]() 天监测了该地空气负离子浓度,并绘制了如图
天监测了该地空气负离子浓度,并绘制了如图![]() 所示的折线图.根据折线图,下列说法错误的是( )
所示的折线图.根据折线图,下列说法错误的是( )
A.这![]() 天的空气负离子浓度总体越来越高
天的空气负离子浓度总体越来越高
B.这![]() 天中空气负离子浓度的中位数约
天中空气负离子浓度的中位数约![]() 个
个![]()
C.后![]() 天的空气质量对身体健康的有利程度明显好于前
天的空气质量对身体健康的有利程度明显好于前![]() 天
天
D.前![]() 天空气质量波动程度小于后
天空气质量波动程度小于后![]() 天
天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国在贵州省平塘县境内修建的500米口径球面射电望远镜(FAST)是目前世界上最大单口径射电望远镜.使用三年来,已发现132颗优质的脉冲星候选体,其中有93颗已被确认为新发现的脉冲星,脉冲星是上世纪60年代天文学的四大发现之一,脉冲星就是正在快速自转的中子星,每一颗脉冲星每两脉冲间隔时间(脉冲星的自转周期)是-定的,最小小到0.0014秒,最长的也不过11.765735秒.某-天文研究机构观测并统计了93颗已被确认为新发现的脉冲星的自转周期,绘制了如图的频率分布直方图.

(1)在93颗新发现的脉冲星中,自转周期在2至10秒的大约有多少颗?
(2)根据频率分布直方图,求新发现脉冲星自转周期的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 作倾斜角为
作倾斜角为![]() 的直线与
的直线与![]() 轴和双曲线的右支分别交于
轴和双曲线的右支分别交于![]() 两点,若点
两点,若点![]() 平分线段
平分线段![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com