
【题目】双曲线![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 作倾斜角为
作倾斜角为![]() 的直线与
的直线与![]() 轴和双曲线的右支分别交于
轴和双曲线的右支分别交于![]() 两点,若点
两点,若点![]() 平分线段
平分线段![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
【答案】B
【解析】双曲线![]()
![]() 的左焦点
的左焦点![]() 为
为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,令
,令![]() ,则
,则![]() ,即
,即![]() ,因为
,因为![]() 平分线段
平分线段![]() ,根据中点坐标公式可得
,根据中点坐标公式可得 ![]() ,代入双曲线方程,可得
,代入双曲线方程,可得![]() ,由于
,由于![]() ,则
,则![]() ,化简可得
,化简可得![]() ,解得
,解得![]() ,由
,由![]() ,解得
,解得![]() ,故选B.
,故选B.
【方法点晴】本题主要考查利用双曲线的简单性质求双曲线的离心率,属于中档题.求解与双曲线性质有关的问题时要结合图形进行分析,既使不画出图形,思考时也要联想到图形,当涉及顶点、焦点、实轴、虚轴、渐近线等双曲线的基本量时,要理清它们之间的关系,挖掘出它们之间的内在联系.求离心率问题应先将 ![]() 用有关的一些量表示出来,再利用其中的一些关系构造出关于
用有关的一些量表示出来,再利用其中的一些关系构造出关于![]() 的等式,从而求出
的等式,从而求出![]() 的值.本题是利用点到直线的距离等于圆半径构造出关于
的值.本题是利用点到直线的距离等于圆半径构造出关于![]() 的等式,最后解出
的等式,最后解出![]() 的值.
的值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长是短轴长的
的长轴长是短轴长的![]() 倍,且过点
倍,且过点![]() .
.
(1)求椭圆的标准方程;
(2)若![]() 的顶点
的顶点![]() 、
、![]() 在椭圆上,
在椭圆上, ![]() 所在的直线斜率为
所在的直线斜率为![]() ,
, ![]() 所在的直线斜率为
所在的直线斜率为![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两焦点与短轴的一个端点的连线构成等腰直角三角形,
的两焦点与短轴的一个端点的连线构成等腰直角三角形,
直线![]() 与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆C上一点,若过点![]() 的直线
的直线![]() 与椭圆C相交于不同的两点S和T,
与椭圆C相交于不同的两点S和T,
满足![]() (O为坐标原点),求实数
(O为坐标原点),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 10 | |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | ||
合计 | 50 |
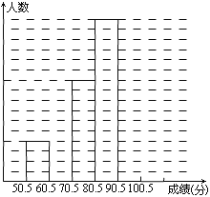
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享自行车”在很多城市相继出现.某运营公司为了了解某地区用户对其所提供的服务的满意度,随机调查了40个用户,得到用户的满意度评分如下:

用系统抽样法从40名用户中抽取容量为10的样本,且在第一分段里随机抽到的评分数据为92.
(1)请你列出抽到的10个样本的评分数据;
(2)计算所抽到的10个样本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)条件下,若用户的满意度评分在![]() 之间,则满意度等级为“
之间,则满意度等级为“![]() 级”.试应用样本估计总体的思想,估计该地区满意度等级为“
级”.试应用样本估计总体的思想,估计该地区满意度等级为“![]() 级”的用户所占的百分比是多少?(精确到
级”的用户所占的百分比是多少?(精确到![]() )
)
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图示.
分组的频率分布直方图如图示.

(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为![]() ,
,![]() ,
,![]() 的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在
的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】编号分别为![]() 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
(1)将得分在对应区间内的人数填入相应的空格:
区间 | [10,20) | [20,30) | [30,40] |
人数 |
(2)从得分在区间[20,30)内的运动员中随机抽取2人.
(ⅰ)用运动员编号列出所有可能的抽取结果;
(ⅱ)求这2人得分之和大于50的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 经过点
经过点![]() ,其中
,其中![]() 为椭圆
为椭圆![]() 的离心率.过点
的离心率.过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(
两点(![]() 在
在![]() 轴下方).
轴下方).
(1)求椭圆![]() 的方程;
的方程;
(2)过原点![]() 且平行于
且平行于![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
, ![]() ,求
,求![]() 的值;
的值;
(3)记直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .若
.若![]() ,求直线
,求直线![]() 的斜率
的斜率![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com