
分析 (1)由已知利用二倍角的余弦函数公式,三角形内角和定理,诱导公式化简可得2cos2A+3cosA-2=0,解得cosA的值,结合范围0<A<π,即可得解A的值.
(2)由已知及正弦定理可求a=2RsinA=$\sqrt{3}$,又利用余弦定理,基本不等式可得bc≤3,利用三角形面积公式即可得解三角形面积的最大值.
解答 (本题满分为12分)
解:(1)∵cos2A-3cos(B+C)-1=0.
∴2cos2A+3cosA-2=0,…2分
∴解得:cosA=$\frac{1}{2}$,或-2(舍去),…4分
又∵0<A<π,
∴A=$\frac{π}{3}$…6分
(2)∵a=2RsinA=$\sqrt{3}$,…(8分)
又∵a2=b2+c2-2bccosA=b2+c2-bc≥bc,
∴bc≤3,当且仅当b=c时取等号,…(10分)
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{4}$bc≤$\frac{3\sqrt{3}}{4}$,
∴三角形面积的最大值为$\frac{3\sqrt{3}}{4}$. …(12分)
点评 本题主要考查了二倍角的余弦函数公式,三角形内角和定理,诱导公式,正弦定理,余弦定理,基本不等式,三角形面积公式在解三角形中的应用,考查了转化思想,属于基础题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:解答题
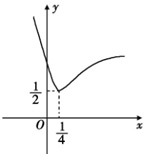 如图所示的函数F(x)的图象,由指数函数f(x)=ax与幂函数g(x)=xb“拼接”而成.
如图所示的函数F(x)的图象,由指数函数f(x)=ax与幂函数g(x)=xb“拼接”而成.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
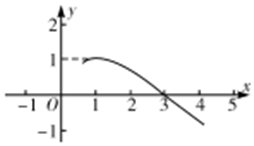
| A. | ω=$\frac{π}{4}$,φ=$\frac{3π}{4}$ | B. | ω=$\frac{π}{4}$,φ=$\frac{π}{4}$ | C. | ω=$\frac{π}{2}$,φ=$\frac{π}{4}$ | D. | ω=$\frac{π}{3}$,φ=$\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com