解:(Ⅰ)
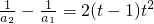
,
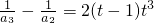
,…
n≥2时,

.
将上面n-1个等式相加,得
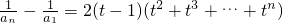
,
得
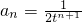
(n≥2).n≥2时,(3分)
又n=1时,
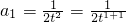
∴对n∈N
*,恒有
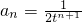
.(4分)
(Ⅱ)

.
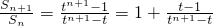
.
又
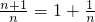
,
所以要证明
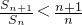
,只需证明
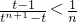
,
即证明t
n+1-(t-1)n-t>0.(6分)
下面证明:t
n+1-(t-1)n-t>0.
(方法一)数学归纳法:
证明:①当n=1时,∵t≥2,∴t
2-2t+1=(t-1)
2>0,命题成立.
②假设当n=k时,命题成立,即t
k+1-(t-1)k-t>0,
那么当n=k+1时,∵t
k+1-(t-1)k-t>0,∴t
k+2-(t
2-t)k-t
2>0
∴t
k+2-(t-1)(k+1)-t>(t
2-t)k+t
2-(t-1)(k+1)-t=(t-1)
2k+(t-1)
2>0,命题也成立.
综上所述对于n∈N
•,命题都成立,
∴t
n+1-(t-1)n-t>0,
∴
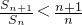
.…(8分)
(方法二)∵n≥1,∴n+1≥2,
∴t
n+1=[1+(t-1)]
n+1=C
n+10+C
n+11(t-1)+C
n+12(t-1)
2+…+C
n+1n+1(t-1)
n+1>C
n+10+C
n+11(t-1)
=1+(n+1)(t-1)
=(t-1)n+t.
∴t
n+1-(t-1)n-t>0,∴
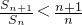
.(8分)
(方法三)令f(x)=t
x+1-[(t-1)x+t](x≥1),
∴f′(x)=t
x+1lnt-t+1>0,
∴f(x)在(0,+∞)是单调递增函数,
∴对于x≥1,总有f(x)≥f(1)=(t-1)
2>0,
从而对于n∈N
*,t
n+1-(t-1)n-t>0成立,
∴
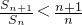
.(8分)
(方法四)要证明
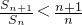
,只需证明
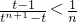
,只需证明
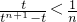
,
只需证明

,即只需证明t
n>n+1,构造函数f(x)=t
x-t-1(x≥1),
则 f′(x)=t
xlnt-1>0,
∴f(x)在[1,+∞)是单调递增函数,∴f(x)≥f(1)=t-2≥0,
∴由以上分析法可知:t
n>n+1,∴
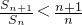
.(8分)
(Ⅲ)由(Ⅰ)知b
n=2
n,∴
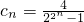
,
∴
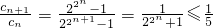
.(9分)
当n=1时,显然
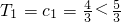
.
当n>1时,
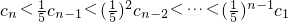
.(10分)
∴
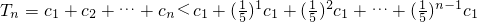
=
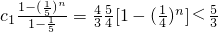
.(12分)
分析:(Ⅰ)依据条件中的等式,分别令n=1,2,…得到
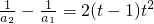
,
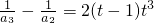
,…n≥2时,

.将上面n-1个等式相加,即可得到通项公式;
(Ⅱ)先利用等比数列的求和公式求出Sn,从而得出
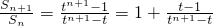
.又
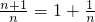
,
所以要证明
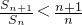
,只需证明
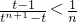
,即证明t
n+1-(t-1)n-t>0.下面证明:t
n+1-(t-1)n-t>0.
(方法一)数学归纳法:证明:①当n=1时,命题成立.②假设当n=k时,命题成立,证明当n=k+1时,命题也成立.
(方法二)∵n≥1,∴n+1≥2,利用二项式定理t
n+1=[1+(t-1)]
n+1进行证明;
(方法三)令f(x)=t
x+1-[(t-1)x+t](x≥1),利用导数工具研究其单调性,从而得到证明;
(方法四)利用分析法证明:要证明
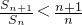
,只需证明
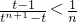
,只需证明
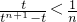
,只需证明

,即只需证明t
n>n+1,最后利用函数的单调性即得.
(Ⅲ)由(Ⅰ)知b
n=2
n,求得
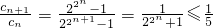
,再结合等比数列的求和公式即可证得结论.
点评:本小题主要考查函数单调性的应用、数列递推式、数学归纳法、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

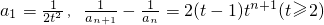 .
.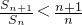 ;
;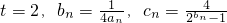 ,设数列{cn}前n项和为Tn,求证:对n∈N*,恒有
,设数列{cn}前n项和为Tn,求证:对n∈N*,恒有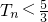 .
.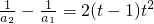 ,
,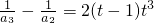 ,…
,… .
.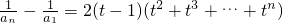 ,
,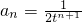 (n≥2).n≥2时,(3分)
(n≥2).n≥2时,(3分)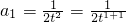 ∴对n∈N*,恒有
∴对n∈N*,恒有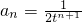 .(4分)
.(4分) .
.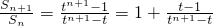 .
.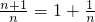 ,
,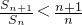 ,只需证明
,只需证明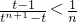 ,
,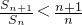 .…(8分)
.…(8分)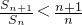 .(8分)
.(8分)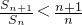 .(8分)
.(8分)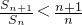 ,只需证明
,只需证明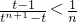 ,只需证明
,只需证明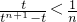 ,
, ,即只需证明tn>n+1,构造函数f(x)=tx-t-1(x≥1),
,即只需证明tn>n+1,构造函数f(x)=tx-t-1(x≥1),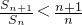 .(8分)
.(8分)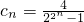 ,
,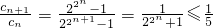 .(9分)
.(9分)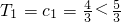 .
.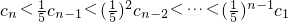 .(10分)
.(10分)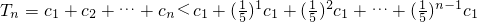
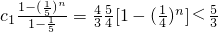 .(12分)
.(12分)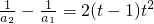 ,
,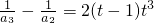 ,…n≥2时,
,…n≥2时, .将上面n-1个等式相加,即可得到通项公式;
.将上面n-1个等式相加,即可得到通项公式;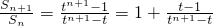 .又
.又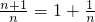 ,
,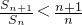 ,只需证明
,只需证明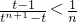 ,即证明tn+1-(t-1)n-t>0.下面证明:tn+1-(t-1)n-t>0.
,即证明tn+1-(t-1)n-t>0.下面证明:tn+1-(t-1)n-t>0.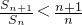 ,只需证明
,只需证明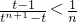 ,只需证明
,只需证明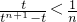 ,只需证明
,只需证明 ,即只需证明tn>n+1,最后利用函数的单调性即得.
,即只需证明tn>n+1,最后利用函数的单调性即得.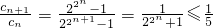 ,再结合等比数列的求和公式即可证得结论.
,再结合等比数列的求和公式即可证得结论.

 优学名师名题系列答案
优学名师名题系列答案