
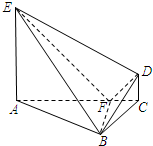
 (2012•漳州模拟)如图,在Rt△ABC中,∠ABC=3∠BAC=90°,BF⊥AC垂足是F,AE⊥平面ABC,CD∥AE,AC=4CD=4,AE=3.
(2012•漳州模拟)如图,在Rt△ABC中,∠ABC=3∠BAC=90°,BF⊥AC垂足是F,AE⊥平面ABC,CD∥AE,AC=4CD=4,AE=3.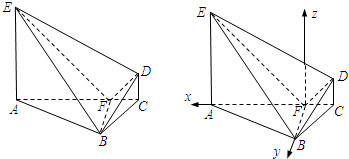 (Ⅰ)证明:∵AE⊥平面ABC,AE?平面AEC,
(Ⅰ)证明:∵AE⊥平面ABC,AE?平面AEC,| 1 |
| 2 |
| 3 |
| BD |
| 3 |
| BE |
| 3 |
| FB |
| 3 |
| FB |
| n |
|
| n |
| 3 |
| n |
| FB |
| ||||
|
|
| 3 | ||||
2
|
| ||
| 4 |
| ||
| 4 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•漳州模拟)如图是某社区工会对当地企业工人月收入情况进行一次抽样调查后画出的频率分布直方图,其中第二组月收入在[1.5,2)千元的频数为300,则此次抽样的样本容量为( )
(2012•漳州模拟)如图是某社区工会对当地企业工人月收入情况进行一次抽样调查后画出的频率分布直方图,其中第二组月收入在[1.5,2)千元的频数为300,则此次抽样的样本容量为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com