
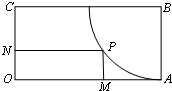
 (2012•闵行区一模)如图,矩形OABC中,AB=1,OA=2,以B为圆心、BA为半径在矩形内部作弧,点P是弧上一动点,PM⊥OA,垂足为M,PN⊥OC,垂足为N,则四边形OMPN的周长的最小值为
(2012•闵行区一模)如图,矩形OABC中,AB=1,OA=2,以B为圆心、BA为半径在矩形内部作弧,点P是弧上一动点,PM⊥OA,垂足为M,PN⊥OC,垂足为N,则四边形OMPN的周长的最小值为| 2 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| 2 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•闵行区一模)在一圆周上给定1000个点.(如图)取其中一点标记上数1,从这点开始按顺时针方向数到第二个点标记上数2,从标记上2的点开始按顺时针方向数到第三个点标记上数3,继续这个过程直到1,2,3,…,2012都被标记到点上,圆周上这些点中有些可能会标记上不止一个数,在标记上2012的那一点上的所有标记的数中最小的是
(2012•闵行区一模)在一圆周上给定1000个点.(如图)取其中一点标记上数1,从这点开始按顺时针方向数到第二个点标记上数2,从标记上2的点开始按顺时针方向数到第三个点标记上数3,继续这个过程直到1,2,3,…,2012都被标记到点上,圆周上这些点中有些可能会标记上不止一个数,在标记上2012的那一点上的所有标记的数中最小的是查看答案和解析>>
科目:高中数学 来源: 题型:
| 1+m2 |
| x | 2 1 |
| x | 2 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•闵行区一模)将边长分别为1、2、3、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.容易知道第1个阴影部分图形的周长为8.设前n个阴影部分图形的周长的平均值为f(n),记数列{an}满足an=
(2012•闵行区一模)将边长分别为1、2、3、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.容易知道第1个阴影部分图形的周长为8.设前n个阴影部分图形的周长的平均值为f(n),记数列{an}满足an=
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com