练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    台风中心从A地以20km/h的速度向东北方向移动，离台风中心30km内的地区为危险区，城市B在A地正东40km处，求城市B处于危险区内的时间．
    分析：根据题意画出相应的图形，如图所示，得出BE=BF=30km，三角形ABD为等腰直角三角形，由|AB|的长求出|BD|的长，作BD垂直于AD，利用三线合一得出|ED|=|FD|，在直角三角形CED中，根据勾股定理求出|ED|的长，进而确定出|EF|的长，除以速度即可求出城市B处于危险区的时间．
    解答：解：根据题意画出相应的图形，如图所示，可得BE=BF=30km，
    △ABD为等腰直角三角形，且AB=40km，
    ∴根据勾股定理得：AD=BD=20
    		2
    km，
    作BD⊥AD，可得ED=FD，
    在Rt△CED中，根据勾股定理得：ED=
    		BE2-BD2
    =10km，
    ∴EF=2ED=20km，
    则城市B处于危险区内的时间为20÷20=1（h）．
    点评：此题考查了直线与圆的位置关系，做出相应的图形是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    台风中心从A地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B在A的正东40千米处，则B城市处于危险区内的时间为（　　）
    A、0.5小时B、1小时C、1.5小时D、2小时

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    台风中心从A地以20 km/h的速度向东北方向移动，离台风中心30 km内的地区为危险区，城市B在A的正东40 km处，B城市处于危险区内的时间为（    ）

    A.0.5 h            B.1 h              C.1.5 h                D.2 h

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    台风中心从A地以20 km/h的速度向东北方向移动,离台风中心30 km内的地区为危险区,城市B在A的正东40 km处,B城市处于危险区内的时间为(    )

    A.0.5 h                B.1 h                C.1.5 h                D.2 h

    查看答案和解析>>

    科目：高中数学 来源：2006年高考第一轮复习数学：5.5 向量的应用（解析版） 题型：选择题

    台风中心从A地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B在A的正东40千米处，则B城市处于危险区内的时间为（ ）
    A．0.5小时
    B．1小时
    C．1.5小时
    D．2小时

    查看答案和解析>>

    科目：高中数学 来源：2010-2011年福建师大附中高一第二学期模块考试数学 题型：解答题

    （本小题满分12分）

    如图，台风中心从A地以每小时20千米的速度向东北方向（北偏东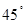）移动，离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系，解决以下问题：

    (1) 求台风移动路径所在的直线方程;

    (2)求城市B处于危险区域的时间是多少小时？

     

     

    查看答案和解析>>

    同步练习册答案