
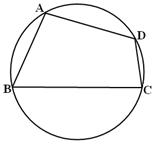
怀化市某棚户区改造工程规划用地近似为图中半径为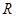 的圆面,图中圆内接四边形
的圆面,图中圆内接四边形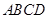 为拟定拆迁的棚户区,测得
为拟定拆迁的棚户区,测得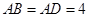 百米,
百米,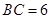 百米,
百米,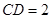 百米.
百米.
(Ⅰ)请计算原棚户区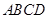 的面积及圆面的半径
的面积及圆面的半径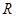 ;
;
(Ⅱ)因地理条件的限制,边界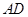 ,
,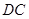 不能变更,而边界
不能变更,而边界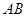 ,
,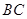 可以调整,为了提高棚户区改造建设用地的利用率,请在圆弧
可以调整,为了提高棚户区改造建设用地的利用率,请在圆弧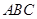 上求出一点
上求出一点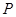 ,使得棚户区改造的新建筑用地
,使得棚户区改造的新建筑用地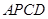 的面积最大,并求最大值.
的面积最大,并求最大值.
科目:高中数学 来源: 题型:
 长沙市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.
长沙市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.查看答案和解析>>
科目:高中数学 来源:2011届重庆市西南师大附中高三期中考试理科数学卷 题型:解答题
重庆市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB =" AD" = 4万米,BC = 6万米,CD = 2万米,
(1)请计算原棚户区建筑用地ABCD的面积及圆面的半径R的值;
(2)因地理条件的限制,边界AD、DC不能变更,而边界AB、BC可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧ABC上设计一点P,使得棚户区改造的新建筑用地APCD的面积最大,并求最大值.
查看答案和解析>>
科目:高中数学 来源:湖南省长沙市一中2010届高三第三次月考(理) 题型:解答题
 长沙市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB = AD = 4万米,BC = 6万米,CD = 2万米.
长沙市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB = AD = 4万米,BC = 6万米,CD = 2万米.
(1)请计算原棚户区建筑用地ABCD的面积及圆面的半径R的值;
(2)因地理条件的限制,边界AD、DC不能变更,而边界AB、BC可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧 上设计一点P;使得棚户区改造的新建筑用地APCD的面积最大,并求最大值.
上设计一点P;使得棚户区改造的新建筑用地APCD的面积最大,并求最大值.
查看答案和解析>>
科目:高中数学 来源:2011年高考数学复习:3 三角函数、解三角形 质量检测(2)(解析版) 题型:解答题
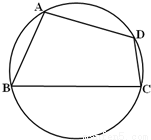 长沙市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.
长沙市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com