【题目】已知f（x）=|x|（2﹣x）
（1）作出函数f（x）的大致图象，并指出其单调区间；
（2）若函数f（x）=c恰有三个不同的解，试确定实数c的取值范围．
【答案】
（1）解：f（x）=|x|（2﹣x）= 
，函数的图象如图：
函数的单调增区间（0，1），单调减区间（﹣∞，0），（1，+∞）．
（2）解：函数f（x）=c恰有三个不同的解，函数在x=1时取得极大值：1，
实数c的取值范围（0，1）．
【解析】（1）化简函数的表达式，然后画出函数的图象，写出单调区间即可．（2）利用函数的图象，推出实数c的取值范围．
【考点精析】本题主要考查了函数的图象的相关知识点，需要掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值才能正确解答此题．
期末宝典单元检测分类复习卷系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ax2+2ax+4（0＜a＜3），若x1＜x2 ， x1+x2=1﹣a，则（ ）
A.f（x1）＜f（x2）
B.f（x1）＞f（x2）
C.f（x1）=f（x2）
D.f（x1）＜f（x2）和f（x1）=f（x2）都有可能
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}满足a1=4，an+1=3an﹣2（n∈N+）
（1）求证：数列{an﹣1}为等比数列，并求出数列{an}的通项公式；
（2）令bn=log3（a1﹣1）+log3（a2﹣1）+…+log3（an﹣1），求数列{ 
}的前n项和Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）=ax2+（b﹣2）x+3（a≠0）
（1）若不等式f（x）＞0的解集（﹣1，3）．求a，b的值；
（2）若f（1）=2，a＞0，b＞0求 
+ 
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱锥A﹣BCD中，侧面ABC是一个等腰直角三角形，∠BAC=90°，底面BCD是一个等边三角形，平面ABC⊥平面BCD，E为BD的中点，则AE与平面BCD所成角的大小为 ． 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，矩形草坪AMPN中，点C在对角线MN上．CD垂直于AN于点D，CB垂直于AM于点B，|CD|=|AB|=3米，|AD|=|BC|=2米，设|DN|=x米，|BM|=y米．求这块矩形草坪AMPN面积的最小值．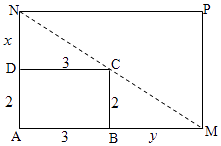 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ln（a﹣ 
）（a∈R）．若关于x的方程ln[（4﹣a）x+2a﹣5]﹣f（x）=0的解集中恰好有一个元素，则实数a的取值范围为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
