
在三棱锥P-ABC中,△ABC是正三角形,∠PCA= ,D为PA中点,二面角P-AC-B为
,D为PA中点,二面角P-AC-B为 ,PC=2,AB=
,PC=2,AB= .
.
(1)求证AC⊥BD;
(2)求BD与底面ABC所成的角(用反正弦表示);
(3)求三棱锥P-ABC的体积.
|
解 (1)如图,取AC中点E,连结BE,DE,则DE∥PC.由PC⊥AC,知DE⊥AC.由△ABC为正三角形,得BE⊥AC.又DE∩BE=E,所以AC⊥平面DEB,
(2)由AC⊥平面DEB, 由DE⊥AC,BE⊥AC,知∠DEB是二面角P-AC-B的平面角.在△DEB中,DE=1, 由正弦定理,得 ∴sin∠DBE= ∴所求角为arc sin 另一解法是由AC⊥平面DEB, 作DF⊥平面ABC,F是垂足,F在BE的延长线上,∠DBF是DB与平面ABC所成的角. 由DE⊥AC,BE⊥AC,知∠DEB是二面角P-AC-B的平面角. 在 Rt△DBF中,DE= 由余弦定理,知BD= (3)∵AC⊥平面DEB, ∴平面DEB⊥平面PAC. 作B到平面PAC的垂线BG,G为垂足,G在DE的延长线上. 在Rt△BEG中,∠BEG=
或由DF= ∴ |


科目:高中数学 来源: 题型:
(本小题满分12分)
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=PA=a,点O、D分别是AC、PC的中点,OP⊥底面ABC。
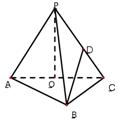
(1)求三棱锥P-ABC的体积;
(2)求异面直线PA与BD所成角余弦值的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.


(1)求证:DE∥平面PBC;
(2)求证:AB⊥PE;
(3)求二面角A-PB-E的大小.
查看答案和解析>>
科目:高中数学 来源:新课标高三数学直线、平面、简单几何体专项训练(河北) 题型:解答题
如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上.

(1)证明:平面PAB⊥平面PCM;
(2)证明:线段PC的中点为球O的球心
查看答案和解析>>
科目:高中数学 来源:岳阳市2010届高三第四次质检考试(数学文)试题 题型:解答题
(本小题满分12分)
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=PA=a,点O、D分别是AC、PC的中点,OP⊥底面ABC。

(1)求三棱锥P-ABC的体积;
(2)求异面直线PA与BD所成角余弦值的大小。
查看答案和解析>>
科目:高中数学 来源:2010-2011年广西南宁沛鸿民族中学高二下学期期中考试数学 题型:解答题
(本小题满分12分)
如图,在三棱锥P-ABC中,PA=PC,∠APC=∠ACB=90°,∠BAC=30°,平面PAC⊥平面ABC.

(1)求证:平面PAB⊥平面PBC;
(2)若PA=2,求三棱锥P-ABC的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com