
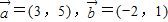
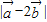 的值;
的值;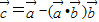 ,求向量
,求向量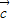 与
与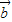 的夹角的余弦值.
的夹角的余弦值.科目:高中数学 来源: 题型:
| a |
| b |
| ||
| 2 |
| 1 |
| 2 |
| a |
| b |
| 9 |
| 5 |
| π |
| 6 |
| 2π |
| 3 |
| 2π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| 3 |
| π |
| 2 |
| a |
| b |
| c |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 4 |
| 5 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三教学质量检测(四)文科数学试卷(解析版) 题型:解答题
(本小题满分12分)设平面向量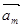 =(m,1),
=(m,1), 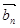 =(2,n),其中m,n∈{1,2,3,4}.
=(2,n),其中m,n∈{1,2,3,4}.
(Ⅰ)请列出有序数组(m,n)的所有可能结果;
(Ⅱ)若“使得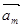 ⊥(
⊥(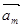 -
-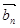 )成立的(m,n)”为事件A,求事件A发生的概率。
)成立的(m,n)”为事件A,求事件A发生的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com