
ЁОЬтФПЁПШчЙћКЏЪ§![]() ЕФЖЈвхгђЮЊ
ЕФЖЈвхгђЮЊ![]() ЃЌЧвДцдкЪЕГЃЪ§
ЃЌЧвДцдкЪЕГЃЪ§![]() ЃЌЪЙЕУЖдгкЖЈвхгђФкШЮвт
ЃЌЪЙЕУЖдгкЖЈвхгђФкШЮвт![]() ЃЌЖМга
ЃЌЖМга![]() ГЩСЂЃЌдђГЦДЫКЏЪ§
ГЩСЂЃЌдђГЦДЫКЏЪ§![]() ОпгаЁАаджЪ
ОпгаЁАаджЪ![]() ЁБ.
ЁБ.
ЃЈ1ЃЉХаЖЯКЏЪ§![]() ЪЧЗёОпгаЁА
ЪЧЗёОпгаЁА![]() аджЪЁБЃЌШєОпгаЁА
аджЪЁБЃЌШєОпгаЁА![]() аджЪЁБЃЌЧѓГіЫљга
аджЪЁБЃЌЧѓГіЫљга![]() ЕФжЕЕФМЏКЯЃЌШєВЛОпгаЁА
ЕФжЕЕФМЏКЯЃЌШєВЛОпгаЁА![]() аджЪЁБЃЌЧыЫЕУїРэгЩЃЛ
аджЪЁБЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉвбжЊКЏЪ§![]() ОпгаЁА
ОпгаЁА![]() аджЪЁБЃЌЧвЕБ
аджЪЁБЃЌЧвЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЧѓКЏЪ§
ЃЌЧѓКЏЪ§![]() дкЧјМф
дкЧјМф![]() ЩЯЕФжЕгђЃЛ
ЩЯЕФжЕгђЃЛ
ЃЈ3ЃЉвбжЊКЏЪ§![]() МШОпгаЁА
МШОпгаЁА![]() аджЪЁБЃЌгжОпгаЁА
аджЪЁБЃЌгжОпгаЁА![]() аджЪЁБЃЌЧвЕБ
аджЪЁБЃЌЧвЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌШєКЏЪ§
ЃЌШєКЏЪ§![]() ЕФЭМЯёгыжБЯп
ЕФЭМЯёгыжБЯп![]() га2017ИіЙЋЙВЕуЃЌЧѓЪЕЪ§
га2017ИіЙЋЙВЕуЃЌЧѓЪЕЪ§![]() ЕФжЕ.
ЕФжЕ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() ЕФжЕгђЮЊ
ЕФжЕгђЮЊ![]() ЃЛ
ЃЛ![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() ЕФжЕгђЮЊ
ЕФжЕгђЮЊ![]() ЃЛ
ЃЛ![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() ЕФжЕгђЮЊ
ЕФжЕгђЮЊ![]() ЃЛ
ЃЛ![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() ЕФжЕгђЮЊ
ЕФжЕгђЮЊ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтПЩжЊ![]() ЃЌгЩД§ЖЈЯЕЪ§ЗЈПЩЧѓЕУ
ЃЌгЩД§ЖЈЯЕЪ§ЗЈПЩЧѓЕУ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩаТЖЈвхПЩЭЦГі![]() ЮЊХМКЏЪ§ЃЌДгЖјЧѓГі
ЮЊХМКЏЪ§ЃЌДгЖјЧѓГі![]() дк
дк![]() ЩЯЕФНтЮіЪНЃЌЬжТлmгы
ЩЯЕФНтЮіЪНЃЌЬжТлmгы![]() ЕФЙиЯЕХаЖЯ
ЕФЙиЯЕХаЖЯ![]() ЕФЕЅЕїадЕУГі
ЕФЕЅЕїадЕУГі![]() ЕФзюжЕЃЛ
ЕФзюжЕЃЛ
ЃЈ3ЃЉИљОнаТЖЈвхПЩжЊ![]() ЮЊжмЦкЮЊ2ЕФХМКЏЪ§ЃЌзїГі
ЮЊжмЦкЮЊ2ЕФХМКЏЪ§ЃЌзїГі![]() ЕФКЏЪ§ЭМЯѓЃЌИљОнКЏЪ§ЭМЯѓЕУГіpЕФжЕ.
ЕФКЏЪ§ЭМЯѓЃЌИљОнКЏЪ§ЭМЯѓЕУГіpЕФжЕ.
ЃЈ1ЃЉМйЩш![]() ОпгаЁА
ОпгаЁА![]() аджЪЁБЃЌдђ
аджЪЁБЃЌдђ![]() КуГЩСЂЃЌ
КуГЩСЂЃЌ
ЕШЪНСНБпЦНЗНећРэЕУЃЌ![]() ЃЌвђЮЊЕШЪНКуГЩСЂЃЌ
ЃЌвђЮЊЕШЪНКуГЩСЂЃЌ
Ыљвд![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
дђЫљга![]() ЕФжЕЕФМЏКЯЮЊ
ЕФжЕЕФМЏКЯЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉвђЮЊКЏЪ§![]() ОпгаЁА
ОпгаЁА![]() аджЪЁБЃЌ
аджЪЁБЃЌ
Ыљвд![]() КуГЩСЂЃЌ
КуГЩСЂЃЌ![]() ЪЧХМКЏЪ§.
ЪЧХМКЏЪ§.
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() .
.
ЂйЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() дк
дк![]() ЩЯЕндіЃЌжЕгђЮЊ
ЩЯЕндіЃЌжЕгђЮЊ![]() .
.
ЂкЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() дк
дк![]() ЩЯЕнМѕЃЌдк
ЩЯЕнМѕЃЌдк![]() ЩЯЕндіЃЌ
ЩЯЕндіЃЌ![]() ЃЌ
ЃЌ![]() ЃЌжЕгђЮЊ
ЃЌжЕгђЮЊ![]() .
.
ЂлЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌжЕгђЮЊ
ЃЌжЕгђЮЊ![]() .
.
Ђм![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() дк
дк![]() ЩЯЕнМѕЃЌжЕгђЮЊ
ЩЯЕнМѕЃЌжЕгђЮЊ![]() .
.
ЃЈ3ЃЉ![]() МШОпгаЁА
МШОпгаЁА![]() аджЪЁБЃЌМД
аджЪЁБЃЌМД![]() ЃЌ
ЃЌ![]() КЏЪ§
КЏЪ§![]() ЮЊХМКЏЪ§ЃЌ
ЮЊХМКЏЪ§ЃЌ
гж![]() МШОпгаЁА
МШОпгаЁА![]() аджЪЁБЃЌМД
аджЪЁБЃЌМД![]() ЃЌ
ЃЌ![]() КЏЪ§
КЏЪ§![]() ЪЧвд2ЮЊжмЦкЕФКЏЪ§.
ЪЧвд2ЮЊжмЦкЕФКЏЪ§.
зїГіКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃК
ЕФЭМЯѓШчЭМЫљЪОЃК
гЩЭМЯѓПЩжЊЃЌЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() гыжБЯп
гыжБЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌМДгаЮоЪ§ИіНЛЕуЃЌВЛКЯЬтвт.
ЃЌМДгаЮоЪ§ИіНЛЕуЃЌВЛКЯЬтвт.
ЕБ![]() ЪБЃЌдкЧјМф
ЪБЃЌдкЧјМф![]() ЩЯЃЌКЏЪ§
ЩЯЃЌКЏЪ§![]() га1008ИіжмЦкЃЌвЊЪЙКЏЪ§
га1008ИіжмЦкЃЌвЊЪЙКЏЪ§![]() ЕФЭМЯѓгыжБЯп
ЕФЭМЯѓгыжБЯп![]() га2017ИіНЛЕуЃЌ
га2017ИіНЛЕуЃЌ
дђжБЯпгыКЏЪ§y=g(x)ЕФЭМЯёдкУПИіжмЦкФкЖМгІга2ИіНЛЕуЃЌЧвЕк2017ИіНЛЕуЧЁКУЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
ЭЌРэЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
злЩЯЃЌ![]() .
.


 ЛЦИдЬьЬьСЗПкЫуЬтПЈЯЕСаД№АИ
ЛЦИдЬьЬьСЗПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABCDЪЧБпГЄЮЊ3ЕФе§ЗНаЮЃЌDEЁЭЦНУцABCDЃЌAFЁЮDEЃЌDE=3AFЃЌBEгыЦНУцABCDЫљГЩНЧЮЊ60ЁуЃЎ
ЃЈЂёЃЉЧѓжЄЃКACЁЭЦНУцBDEЃЛ
ЃЈЂђЃЉЧѓЖўУцНЧFЉBEЉDЕФгрЯвжЕЃЎ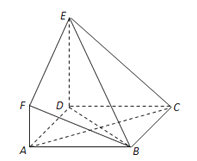
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌПеМфЫФБпаЮABCDжаЃЌAB=CDЃЌABЁЭCDЃЌEЁЂFЗжБ№ЮЊBCЁЂADЕФжаЕуЃЌдђEFКЭABЫљГЩЕФНЧЮЊ 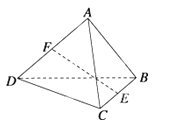
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШчЭМЫљЪОЕФМИКЮЬхжаЃЌAEЁЭЦНУцABCЃЌCDЁЮAEЃЌFЪЧBEЕФжаЕуЃЌAC=BC=1ЃЌЁЯACB=90ЁуЃЌAE=2CD=2ЃЎ
жЄУїDFЁЭЦНУцABEЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхгђЮЊ![]() ЕФКЏЪ§
ЕФКЏЪ§![]() ТњзуЃКЖдгкШЮвтЕФЪЕЪ§
ТњзуЃКЖдгкШЮвтЕФЪЕЪ§![]() ЖМга
ЖМга![]() ГЩСЂЃЌЧвЕБ
ГЩСЂЃЌЧвЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() КуГЩСЂЃЌЧв
КуГЩСЂЃЌЧв![]() ЪЧвЛИіИјЖЈЕФе§ећЪ§ЃЉЃЎ
ЪЧвЛИіИјЖЈЕФе§ећЪ§ЃЉЃЎ
ЃЈ1ЃЉХаЖЯКЏЪ§![]() ЕФЦцХМадЃЌВЂжЄУїФуЕФНсТлЃЛ
ЕФЦцХМадЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ2ЃЉХаЖЯВЂжЄУї![]() ЕФЕЅЕїадЃЛШєКЏЪ§
ЕФЕЅЕїадЃЛШєКЏЪ§![]() дк
дк![]() ЩЯзмга
ЩЯзмга![]() ГЩСЂЃЌЪдШЗЖЈ
ГЩСЂЃЌЪдШЗЖЈ![]() гІТњзуЕФЬѕМўЃЛ
гІТњзуЕФЬѕМўЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌНтЙигк
ЪБЃЌНтЙигк![]() ЕФВЛЕШЪН
ЕФВЛЕШЪН![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтЃКЂйМЏКЯ![]() ЕФзгМЏИіЪ§га
ЕФзгМЏИіЪ§га![]() ИіЃЛЂкЖЈвхдк
ИіЃЛЂкЖЈвхдк![]() ЩЯЕФЦцКЏЪ§
ЩЯЕФЦцКЏЪ§![]() БиТњзу
БиТњзу![]() ЃЛЂл
ЃЛЂл![]() МШВЛЪЧЦцКЏЪ§гжВЛЪЧХМКЏЪ§ЃЛЂмХМКЏЪ§ЕФЭМЯёвЛЖЈгы
МШВЛЪЧЦцКЏЪ§гжВЛЪЧХМКЏЪ§ЃЛЂмХМКЏЪ§ЕФЭМЯёвЛЖЈгы![]() жсЯрНЛЃЛЂн
жсЯрНЛЃЛЂн![]() дк
дк![]() ЩЯЪЧМѕКЏЪ§ЃЌЦфжаецУќЬтЕФађКХЪЧ ______________ЃЈАбФуШЯЮЊе§ШЗЕФУќЬтЕФађКХЖМЬюЩЯЃЉ.
ЩЯЪЧМѕКЏЪ§ЃЌЦфжаецУќЬтЕФађКХЪЧ ______________ЃЈАбФуШЯЮЊе§ШЗЕФУќЬтЕФађКХЖМЬюЩЯЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШ§РтжљABCЉA1B1C1жаЃЌDЃЌEЗжБ№ЪЧB1C1ЁЂBCЕФжаЕуЃЌЁЯBAC=90ЁуЃЌAB=AC=2ЃЌA1A=4ЃЌA1E= ![]() ЃЎ
ЃЎ
ЃЈЂёЃЉжЄУїЃКA1DЁЭЦНУцA1BCЃЛ
ЃЈЂђЃЉЧѓЖўУцНЧAЉBDЉB1ЕФЦНУцНЧЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТСаЫФИіНсТлЃК
ЂйвбжЊXЗўДге§ЬЌЗжВМNЃЈ0ЃЌІв2ЃЉЃЌЧвPЃЈЉ2ЁмXЁм2ЃЉ=0.6ЃЌдђPЃЈXЃО2ЃЉ=0.2ЃЛ
ЂкШєУќЬт ![]() ЃЌдђЉVpЃКxЁЪЃЈЉЁоЃЌ1ЃЉЃЌx2ЉxЉ1Ён0ЃЛ
ЃЌдђЉVpЃКxЁЪЃЈЉЁоЃЌ1ЃЉЃЌx2ЉxЉ1Ён0ЃЛ
ЂлвбжЊжБЯпl1ЃКax+3yЉ1=0ЃЌl2ЃКx+by+1=0ЃЌдђl1ЁЭl2ЕФГфвЊЬѕМўЪЧ ![]() ЃЎ
ЃЎ
Цфжае§ШЗЕФНсТлЕФИіЪ§ЮЊЃЈ ЃЉ
A.0
B.1
C.2
D.3
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com