练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某房地产开发公司计划在一楼区内建造一个长方形公园，公园由长方形的休闲区（阴影部分）和环公园人行道组成.已知休闲区的面积为4000平方米，人行道的宽分别为4米和10米.

    （1）若设休闲区的长米，求公园所占面积关于的函数的解析式；

    （2）要使公园所占面积最小，休闲区的长和宽该如何设计？

    【答案】（1）；（2）要使公园所占面积最小，休闲区的长为100米，宽为40米.

    【解析】试题分析：本题为函数应用问题，首先要要认真细致的审题，逐字逐句的读题，建立函数模型，把实际问题转化为数学问题.注意函数的定义域，实际问题要注意实际要求，建立函数关系后，有时利用基本不等式求最值，但要注意等号成立的条件，有时利用二次函数求最值,有时还需要借助导数研究函数的单调性求最值.

    试题解析：

    由，知

    （2）

    当且仅当即时取等号

    ∴要使公园所占面积最小，休闲区的长为100米，宽为40米.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和为， ，数列满足点在直线上.

    (1)求数列， 的通项， ；

    (2)令，求数列的前项和；

    (3)若，求对所有的正整数都有成立的的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足， ，其中， ， 为非零常数.

    （1）若， ，求证： 为等比数列，并求数列的通项公式；

    （2）若数列是公差不等于零的等差数列.

    ①求实数， 的值；

    ②数列的前项和构成数列，从中取不同的四项按从小到大排列组成四项子数列.试问：是否存在首项为的四项子数列，使得该子数列中的所有项之和恰好为2017？若存在，求出所有满足条件的四项子数列；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】双“十一”结束之后，某网站针对购物情况进行了调查，参与调查的人主要集中在[20，50]岁之间，若规定：购物600（含600元）以下者，称为“理智购物”，购物超过600元者被网友形象的称为“剁手党”，得到如下统计表：

    分组编号

    年龄分组

    球迷

    所占比例

    1

    [20，25）

    1000

    0.5

    2

    [25，30）

    1800

    0.6

    3

    [30，35）

    1200

    0.5

    4

    [35，40）

    a

    0.4

    5

    [40，45）

    300

    0.2

    6

    [45，50]

    200

    0.1

    若参与调查的“理智购物”总人数为7720人．
    （1）求a的值；
    （2）从年龄在[20，35）的“剁手党”中按照年龄区间分层抽样的方法抽取20人； ①从这20人中随机抽取2人，求这2人恰好属于同一年龄区间的概率；
    ②从这20人中随机抽取2人，用ζ表示年龄在[20，25）之间的人数，求ξ的分布列及期望值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知的角所对的边份别为，且

    （1）求角的大小；

    （2）若，求的周长的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x（lnx﹣ax）．
    （1）a= 时，求f（x）在点（1，f（1））处的切线方程；
    （2）若f（x）存在两个不同的极值x1 ， x2 ， 求a的取值范围；
    （3）在（2）的条件下，求f（x）在（0，a]上的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，点A是以线段BC为直径的圆O上一点，AD⊥BC于点D，过点B作圆O的切线，与CA的延长线相交于点E，点G是AD的中点，连接CG并延长与BE相交于点F，延长AF与CB的延长线相交于点P．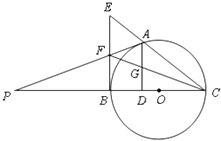
    （1）求证：BF=EF；
    （2）求证：PA是圆O的切线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知公差不为0的等差数列{an}的前n项和为Sn， S3＝a4＋6，且a1， a4， a13成等比数列.

    (1)求数列{an}的通项公式；

    (2)设，求数列{bn}的前n项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程，并对全校学生的选择意向进行调查(调查要求全员参与，每个学生必须从八门课程中选出唯一一门课程).本次调查结果整理成条形图如下.

    上图中，已知课程为人文类课程，课程为自然科学类课程.为进一步研究学生选课意向，结合上面图表，采取分层抽样方法从全校抽取的学生作为研究样本组(以下简称“组M”).

    (Ⅰ)在“组M”中，选择人文类课程和自然科学类课程的人数各有多少？

    (Ⅱ)为参加某地举办的自然科学营活动，从“组M”所有选择自然科学类课程的同学中随机抽取4名同学前往，其中选择课程F或课程H的同学参加本次活动，费用为每人1500元，选择课程G的同学参加，费用为每人2000元.

    (ⅰ)设随机变量表示选出的4名同学中选择课程的人数，求随机变量的分布列；

    (ⅱ)设随机变量表示选出的4名同学参加科学营的费用总和，求随机变量的期望.

    查看答案和解析>>

    同步练习册答案