
【题目】如图,点A是以线段BC为直径的圆O上一点,AD⊥BC于点D,过点B作圆O的切线,与CA的延长线相交于点E,点G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P. 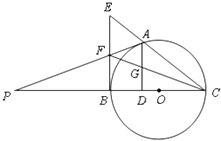
(1)求证:BF=EF;
(2)求证:PA是圆O的切线.
【答案】
(1)证明:∵BC是圆O的直径,BE是圆O的切线,∴EB⊥BC.
又∵AD⊥BC,∴AD∥BE.
可得△BFC∽△DGC,△FEC∽△GAC.
∴ ![]() ,得
,得 ![]() .
.
∵G是AD的中点,即DG=AG.
∴BF=EF
(2)证明:连接AO,AB.

∵BC是圆O的直径,∴∠BAC=90°.
由(1)得:在Rt△BAE中,F是斜边BE的中点,
∴AF=FB=EF,可得∠FBA=∠FAB.
又∵OA=OB,∴∠ABO=∠BAO.
∵BE是圆O的切线,
∴∠EBO=90°,得∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°,
∴PA⊥OA,由圆的切线判定定理,得PA是圆O的切线.
【解析】(1)利用平行线截三角形得相似三角形,得△BFC∽△DGC且△FEC∽△GAC,得到对应线段成比例,再结合已知条件可得BF=EF;(2)利用直角三角形斜边上的中线的性质和等边对等角,得到∠FAO=∠EBO,结合BE是圆的切线,得到PA⊥OA,从而得到PA是圆O的切线.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB,位于该市的某大学M与市中心O的距离OM=3 ![]() km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ=
km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ= ![]() ,AO=15km.
,AO=15km. 
(1)求大学M在站A的距离AM;
(2)求铁路AB段的长AB.
查看答案和解析>>
科目:高中数学 来源: 题型:
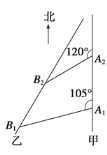
【题目】如图所示,甲船以每小时30![]() 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10![]() 海里.问:乙船每小时航行多少海里?
海里.问:乙船每小时航行多少海里?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发公司计划在一楼区内建造一个长方形公园![]() ,公园由长方形的休闲区
,公园由长方形的休闲区![]() (阴影部分)和环公园人行道组成.已知休闲区
(阴影部分)和环公园人行道组成.已知休闲区![]() 的面积为4000平方米,人行道的宽分别为4米和10米.
的面积为4000平方米,人行道的宽分别为4米和10米.
(1)若设休闲区的长![]() 米,求公园
米,求公园![]() 所占面积
所占面积![]() 关于
关于![]() 的函数
的函数![]() 的解析式;
的解析式;
(2)要使公园所占面积最小,休闲区![]() 的长和宽该如何设计?
的长和宽该如何设计?

查看答案和解析>>
科目:高中数学 来源: 题型:
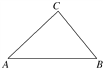
【题目】如图,在△ABC中,已知|AB|=4 ![]() ,且三内角A,B,C满足2sin A+sin C=2sin B,建立适当的坐标系,求顶点C的轨迹方程.
,且三内角A,B,C满足2sin A+sin C=2sin B,建立适当的坐标系,求顶点C的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
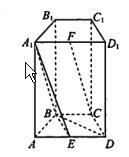
【题目】如图,在四棱柱 ![]() 中,侧面
中,侧面![]() 和侧面
和侧面![]() 都是矩形,
都是矩形, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() 分别为
分别为![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() .
.
(3)若![]() 平面
平面![]() ,求棱
,求棱![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左焦点为
的左焦点为![]() ,
, ![]() 为坐标原点,点
为坐标原点,点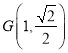 在椭圆上,过点
在椭圆上,过点![]() 的直线
的直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)求弦![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(3)设过点![]() 且不与坐标轴垂直的直线交椭圆于
且不与坐标轴垂直的直线交椭圆于![]() 两点,
两点, ![]() 为
为![]() 轴上一点,若
轴上一点,若![]() 是菱形的两条邻边,求点
是菱形的两条邻边,求点![]() 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com