
【题目】已知函数f(x)=x2﹣6x+8,x∈[1,a],并且函数f(x)的最小值为f(a),则实数a的取值范围是 .
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图所示,ABCD﹣A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1 , B1C1的中点,P是上底面的棱AD上的一点,AP= ![]() ,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= .
,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= . 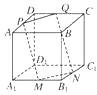
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点A是以线段BC为直径的圆O上一点,AD⊥BC于点D,过点B作圆O的切线,与CA的延长线相交于点E,点G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P. 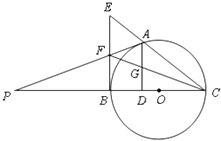
(1)求证:BF=EF;
(2)求证:PA是圆O的切线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为0的等差数列{an}的前n项和为Sn, S3=a4+6,且a1, a4, a13成等比数列.
(1)求数列{an}的通项公式;
(2)设![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题,某单位在国家科研部门的支持下,进行技术攻关,采用了新式艺,把二氧化碳转化为一种可利用的化工产品,已知该单位每月的处理量最少为300吨,最多为600吨,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为![]() ,且每处理一吨二氧化碳得到可利用的化工产品价值为200元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为200元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则需要国家至少补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() .如果对于
.如果对于![]() 的每一个含有
的每一个含有![]() 个元素的子集
个元素的子集![]() ,
, ![]() 中必有4个元素的和等于
中必有4个元素的和等于![]() ,称正整数
,称正整数![]() 为集合
为集合![]() 的一个“相关数”.
的一个“相关数”.
(Ⅰ)当![]() 时,判断5和6是否为集合
时,判断5和6是否为集合![]() 的“相关数”,说明理由;
的“相关数”,说明理由;
(Ⅱ)若![]() 为集合
为集合![]() 的“相关数”,证明:
的“相关数”,证明: ![]() ;
;
(Ⅲ)给定正整数![]() .求集合
.求集合![]() 的“相关数”
的“相关数” ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文科选做)如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E、F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段A1P长度的取值范围是_____。
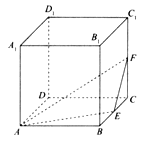
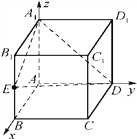
(理科选做)在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com