
【题目】设集合![]() .如果对于
.如果对于![]() 的每一个含有
的每一个含有![]() 个元素的子集
个元素的子集![]() ,
, ![]() 中必有4个元素的和等于
中必有4个元素的和等于![]() ,称正整数
,称正整数![]() 为集合
为集合![]() 的一个“相关数”.
的一个“相关数”.
(Ⅰ)当![]() 时,判断5和6是否为集合
时,判断5和6是否为集合![]() 的“相关数”,说明理由;
的“相关数”,说明理由;
(Ⅱ)若![]() 为集合
为集合![]() 的“相关数”,证明:
的“相关数”,证明: ![]() ;
;
(Ⅲ)给定正整数![]() .求集合
.求集合![]() 的“相关数”
的“相关数” ![]() 的最小值.
的最小值.
【答案】(1)![]() 不是,
不是, ![]() 是(2)见解析(3)
是(2)见解析(3) ![]()
【解析】试题分析:(Ⅰ)由![]() 可得
可得![]() 及
及![]() ,对于
,对于![]() 个元素的子集可以举出反例
个元素的子集可以举出反例![]() 可证含有
可证含有![]() 个元素的子集只有
个元素的子集只有![]() ,满足题意;(Ⅱ)首先考察集合
,满足题意;(Ⅱ)首先考察集合![]() 的含有
的含有![]() 个元素的子集
个元素的子集![]() ,证明当
,证明当![]() 时,
时, ![]() 一定不是集合
一定不是集合![]() 的“相关数”,可得结果;(Ⅲ)先将集合
的“相关数”,可得结果;(Ⅲ)先将集合![]() 的元素分成如下
的元素分成如下![]() 组:
组: ![]() ,再将集合
,再将集合![]() 的元素剔除
的元素剔除![]() 和
和![]() 后,分成如下
后,分成如下![]() 组:
组: ![]() ,可得两者中同属对于
,可得两者中同属对于![]() 的一个含有
的一个含有![]() 个元素的子集
个元素的子集![]() 中至少一组无相同元素,可得结果.
中至少一组无相同元素,可得结果.
试题解析:(Ⅰ)当![]() 时,
时, ![]() ,
, ![]() .①对于
.①对于![]() 的含有
的含有![]() 个元素的子集
个元素的子集![]() ,因为
,因为![]() ,所以
,所以![]() 不是集合
不是集合![]() 的“相关数”.
的“相关数”.
②![]() 的含有
的含有![]() 个元素的子集只有
个元素的子集只有![]() ,因为
,因为![]() ,
,
所以![]() 是集合
是集合![]() 的“相关数”.
的“相关数”.
(Ⅱ)考察集合![]() 的含有
的含有![]() 个元素的子集
个元素的子集![]() .
.
![]() 中任意
中任意![]() 个元素之和一定不小于
个元素之和一定不小于![]() .
.
所以![]() 一定不是集合
一定不是集合![]() 的“相关数”.
的“相关数”.
所以当![]() 时,
时, ![]() 一定不是集合
一定不是集合![]() 的“相关数”.
的“相关数”.
因此若![]() 为集合
为集合![]() 的“相关数”,必有
的“相关数”,必有![]() .
.
即若![]() 为集合
为集合![]() 的“相关数”,必有
的“相关数”,必有![]() .
.
(Ⅲ)由(Ⅱ)得 ![]() .先将集合
.先将集合![]() 的元素分成如下
的元素分成如下![]() 组:
组:
![]() .对
.对![]() 的任意一个含有
的任意一个含有![]() 个元素的子集
个元素的子集![]() ,必有三组
,必有三组![]() 同属于集合
同属于集合![]() .再将集合
.再将集合![]() 的元素剔除
的元素剔除![]() 和
和![]() 后,分成如下
后,分成如下![]() 组:
组:
![]() .对于
.对于![]() 的任意一个含有
的任意一个含有![]() 个元素的子集
个元素的子集![]() ,必有一组
,必有一组![]() 属于集合
属于集合![]() .这一组
.这一组![]() 与上述三组
与上述三组![]() 中至少一组无相同元素,
中至少一组无相同元素,
不妨设![]() 与
与![]() 无相同元素.此时这
无相同元素.此时这![]() 个元素之和为
个元素之和为![]() .所以集合
.所以集合![]() 的“相关数”
的“相关数”![]() 的最小值为
的最小值为![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
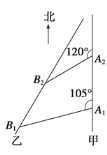
【题目】如图所示,甲船以每小时30![]() 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10![]() 海里.问:乙船每小时航行多少海里?
海里.问:乙船每小时航行多少海里?
查看答案和解析>>
科目:高中数学 来源: 题型:
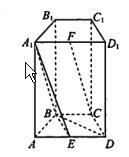
【题目】如图,在四棱柱 ![]() 中,侧面
中,侧面![]() 和侧面
和侧面![]() 都是矩形,
都是矩形, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() 分别为
分别为![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() .
.
(3)若![]() 平面
平面![]() ,求棱
,求棱![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,(1)已知a=![]() ,b=
,b=![]() ,B=45°,求A、C、c;
,B=45°,求A、C、c;
(2)已知sin A∶sin B∶sin C=(![]() +1)∶(
+1)∶(![]() -1)∶
-1)∶![]() ,求最大角.
,求最大角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点是原点,以
的顶点是原点,以![]() 轴为对称轴,且经过点
轴为对称轴,且经过点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
, ![]() 在抛物线
在抛物线![]() 上,直线
上,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() ,
, ![]() .求直线
.求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有三支股票![]() ,
, ![]() ,
, ![]() ,28位股民的持有情况如下:每位股民至少持有其中一支股票,在不持有
,28位股民的持有情况如下:每位股民至少持有其中一支股票,在不持有![]() 股票的人中,持有
股票的人中,持有![]() 股票的人数是持有
股票的人数是持有![]() 股票的人数的2倍.在持有
股票的人数的2倍.在持有![]() 股票的人中,只持有
股票的人中,只持有![]() 股票的人数比除了持有
股票的人数比除了持有![]() 股票外,同时还持有其它股票的人数多1.在只持有一支股票的人中,有一半持有
股票外,同时还持有其它股票的人数多1.在只持有一支股票的人中,有一半持有![]() 股票.则只持有
股票.则只持有![]() 股票的股民人数是( )
股票的股民人数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左焦点为
的左焦点为![]() ,
, ![]() 为坐标原点,点
为坐标原点,点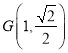 在椭圆上,过点
在椭圆上,过点![]() 的直线
的直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)求弦![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(3)设过点![]() 且不与坐标轴垂直的直线交椭圆于
且不与坐标轴垂直的直线交椭圆于![]() 两点,
两点, ![]() 为
为![]() 轴上一点,若
轴上一点,若![]() 是菱形的两条邻边,求点
是菱形的两条邻边,求点![]() 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).

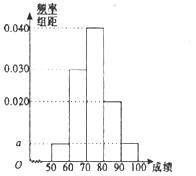
(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式: 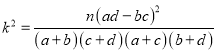 ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com