
【题目】已知椭圆![]() :
: ![]() 的左焦点为
的左焦点为![]() ,
, ![]() 为坐标原点,点
为坐标原点,点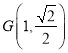 在椭圆上,过点
在椭圆上,过点![]() 的直线
的直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)求弦![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(3)设过点![]() 且不与坐标轴垂直的直线交椭圆于
且不与坐标轴垂直的直线交椭圆于![]() 两点,
两点, ![]() 为
为![]() 轴上一点,若
轴上一点,若![]() 是菱形的两条邻边,求点
是菱形的两条邻边,求点![]() 横坐标的取值范围.
横坐标的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)已知椭圆![]() :
: ![]() 的左焦点为
的左焦点为![]() ,有
,有![]() ,点
,点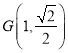 在椭圆上,得
在椭圆上,得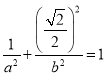 ,联立求出
,联立求出![]() 即得方程(2)设
即得方程(2)设![]() ,
, ![]() ,则
,则![]() ,当
,当![]() 时,
时, ![]() 点的坐标为
点的坐标为![]() . 当
. 当![]() 时,∵
时,∵![]() ,
, ![]() ,点差法两式相减得
,点差法两式相减得![]() ,
,
∴![]() ,又
,又![]() 过
过![]() 点,于是
点,于是![]() 的斜率为
的斜率为![]() ,∴
,∴![]() 整理即可
整理即可
(3)设![]() ,
, ![]() 的中点
的中点![]() ,由(2)知,
,由(2)知, ![]() ①
①
∵![]() ,∴
,∴![]() .∴
.∴![]() ,即
,即![]() ,整理得
,整理得![]() ②将②代入①中,得
②将②代入①中,得![]() ,化为
,化为![]() ,
,
∵![]() ,∴
,∴![]() ,由
,由![]() 得
得![]() 的范围,从而得m的范围.
的范围,从而得m的范围.
试题解析:
(1)由题意有![]() ,且
,且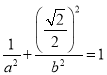 ,解得
,解得![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
, ![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() 点的坐标为
点的坐标为![]() .
.
当![]() 时,∵
时,∵![]() ,
, ![]() ,
,
两式相减得![]() ,
,
∴![]() ,又
,又![]() 过
过![]() 点,于是
点,于是![]() 的斜率为
的斜率为![]() ,
,
∴![]() ,
,
整理得![]() .
.
∵![]() 也满足上式,
也满足上式,
∴![]() 的轨迹方程为
的轨迹方程为![]() .
.
(3)设![]() ,
, ![]() 的中点
的中点![]() ,由(2)知,
,由(2)知, ![]() ①
①
∵![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() ,整理得
,整理得![]() ②
②
将②代入①中,得![]() ,化为
,化为![]() ,
,
∵![]() ,∴
,∴ ![]() ,
,
由![]() (当
(当![]() 时,
时, ![]() 与
与![]() 轴垂直,不合题意,舍去),得
轴垂直,不合题意,舍去),得![]() ,
,
于是![]() ,即
,即![]() 点的横坐标的取值范围为
点的横坐标的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,点A是以线段BC为直径的圆O上一点,AD⊥BC于点D,过点B作圆O的切线,与CA的延长线相交于点E,点G是AD的中点,连接CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P. 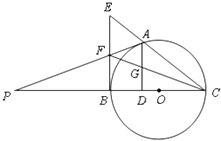
(1)求证:BF=EF;
(2)求证:PA是圆O的切线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() .如果对于
.如果对于![]() 的每一个含有
的每一个含有![]() 个元素的子集
个元素的子集![]() ,
, ![]() 中必有4个元素的和等于
中必有4个元素的和等于![]() ,称正整数
,称正整数![]() 为集合
为集合![]() 的一个“相关数”.
的一个“相关数”.
(Ⅰ)当![]() 时,判断5和6是否为集合
时,判断5和6是否为集合![]() 的“相关数”,说明理由;
的“相关数”,说明理由;
(Ⅱ)若![]() 为集合
为集合![]() 的“相关数”,证明:
的“相关数”,证明: ![]() ;
;
(Ⅲ)给定正整数![]() .求集合
.求集合![]() 的“相关数”
的“相关数” ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选择意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果整理成条形图如下.

上图中,已知课程![]() 为人文类课程,课程
为人文类课程,课程![]() 为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取
为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取![]() 的学生作为研究样本组(以下简称“组M”).
的学生作为研究样本组(以下简称“组M”).
(Ⅰ)在“组M”中,选择人文类课程和自然科学类课程的人数各有多少?
(Ⅱ)为参加某地举办的自然科学营活动,从“组M”所有选择自然科学类课程的同学中随机抽取4名同学前往,其中选择课程F或课程H的同学参加本次活动,费用为每人1500元,选择课程G的同学参加,费用为每人2000元.
(ⅰ)设随机变量![]() 表示选出的4名同学中选择课程
表示选出的4名同学中选择课程![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列;
的分布列;
(ⅱ)设随机变量![]() 表示选出的4名同学参加科学营的费用总和,求随机变量
表示选出的4名同学参加科学营的费用总和,求随机变量![]() 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() +b,其中a,b是常数且a>0.
+b,其中a,b是常数且a>0.
(1)用函数单调性的定义证明f(x)在区间(0, ![]() ]上是单调递减函数;
]上是单调递减函数;
(2)已知函数f(x)在区间[ ![]() ,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值.
,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x≠0).
(x≠0).
(1)证明函数f(x)为奇函数;
(2)判断函数f(x)在[1,+∞)上的单调性,并说明理由;
(3)若x∈[﹣2,﹣3],求函数的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文科选做)如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E、F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段A1P长度的取值范围是_____。
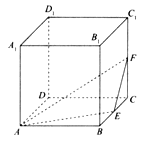
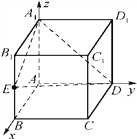
(理科选做)在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+α)(A>0,ω>0,﹣ ![]() <α<
<α< ![]() )的最小正周期是π,且当x=
)的最小正周期是π,且当x= ![]() 时,f(x)取得最大值2.
时,f(x)取得最大值2.
(1)求f(x)的解析式,并作出f(x)在[0,π]上的图象(要列表);
(2)将函数f(x)的图象向右平移m(m>0)个单位长度后得到函数y=g(x)的图象,且y=g(x)是偶函数,求m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式(a2﹣a)4x﹣2x﹣1<0在区间(﹣∞,1]上恒成立,则实数a的取值范围为( )
A.(﹣2, ![]() )
)
B.(﹣∞, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣∞,6]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com