
分析 (Ⅰ)点P($\sqrt{2}$,$\frac{7π}{4}$)在直线l:ρcosθ+2ρcosθ+a=0(a∈R)上,可得$\sqrt{2}$$(cos\frac{7π}{4}+2sin\frac{7π}{4})$+a=0,解得a.再把极坐标化为直角坐标方程即可得出.
(Ⅱ)由题知,对于某点$B(x,\frac{1}{4}{x^2})$,当BA⊥l时,|AB|最小,此时|AB|=$\frac{|x+\frac{1}{2}{x}^{2}+1|}{\sqrt{5}}$=$\frac{\frac{1}{2}(x+1)^{2}+\frac{1}{2}}{\sqrt{5}}$,利用二次函数的单调性即可得出.
解答 解:(Ⅰ)点P($\sqrt{2}$,$\frac{7π}{4}$)在直线l:ρcosθ+2ρcosθ+a=0(a∈R)上,
∴$\sqrt{2}$$(cos\frac{7π}{4}+2sin\frac{7π}{4})$+a=0,
化为$\sqrt{2}$×$(\frac{\sqrt{2}}{2}-2×\frac{\sqrt{2}}{2})$+a=0,解得a=1.
∴直线l:ρcosθ+2ρcosθ+a=0即为:ρcosθ+2ρcosθ+1=0,
可得直角坐标方程:x+2y+1=0.
(Ⅱ)由题知,对于某点$B(x,\frac{1}{4}{x^2})$,
当BA⊥l时,|AB|最小,
此时|AB|=$\frac{|x+\frac{1}{2}{x}^{2}+1|}{\sqrt{5}}$=$\frac{\frac{1}{2}(x+1)^{2}+\frac{1}{2}}{\sqrt{5}}$$≥\frac{1}{2\sqrt{5}}$,
∴|AB|的最小值为$\frac{{\sqrt{5}}}{10}$.
点评 本题考查了极坐标与直角坐标方程互化、点到直线的距离公式、二次函数的性质,考查了推理能力与计算能力,属于中档题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
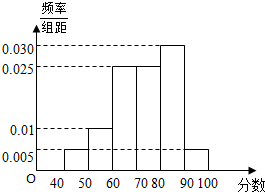 从某校参加高二年级学业水平考试模拟考试的学生中抽取60名学生,将其数学成绩分成6段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]后,画出如图的频率分布直方图.根据图形信息,解答下列问题:
从某校参加高二年级学业水平考试模拟考试的学生中抽取60名学生,将其数学成绩分成6段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]后,画出如图的频率分布直方图.根据图形信息,解答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
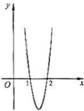 已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求:
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com