
分析 (1)由直线l经过点P(-1,0),且倾斜角为α,利用点斜式可得直线方程.曲线C的极坐标方程为ρ=2cosθ,即ρ2=2ρcosθ,利用互化公式可得直角坐标方程.由直线l与曲线C有公共点,可得$\frac{|2tanα|}{\sqrt{1+ta{n}^{2}α}}$≤1,解出即可得出.
(2)圆心到直线的距离d=$\frac{1}{2}$,可得弦长=2$\sqrt{{r}^{2}-{d}^{2}}$.
解答 解:(1)由直线l经过点P(-1,0),且倾斜角为α,可得直线方程:y=(x+1)tanα,
曲线C的极坐标方程为ρ=2cosθ,即ρ2=2ρcosθ,可得直角坐标方程:x2+y2-2x=0,可得(x-1)2+y2=1,
∵直线l与曲线C有公共点,∴$\frac{|2tanα|}{\sqrt{1+ta{n}^{2}α}}$≤1,可得:tan2α≤$\frac{1}{3}$,∴$-\frac{\sqrt{3}}{3}$≤tanα≤$\frac{\sqrt{3}}{3}$,
∵α∈[0,π),∴α∈$[0,\frac{π}{6}]$∪$[\frac{5π}{6},π)$.
(2)圆心到直线的距离d=$\frac{1}{2}$,
∴直线l1:x-$\sqrt{3}$y=0被曲线C所截得的弦长L=2$\sqrt{1-(\frac{1}{2})^{2}}$=$\sqrt{3}$.
点评 本题考查了曲线的相交弦长、极坐标化为直角坐标方程、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
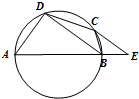
| A. | 160° | B. | 150° | C. | 140° | D. | 130° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com