
【题目】记![]() ,其中
,其中![]() 为函数
为函数![]() 的导数
的导数![]() 若对于
若对于![]() ,
,![]() ,则称函数
,则称函数![]() 为D上的凸函数.
为D上的凸函数.
![]() 求证:函数
求证:函数![]() 是定义域上的凸函数;
是定义域上的凸函数;
![]() 已知函数
已知函数![]() ,
,![]() 为
为![]() 上的凸函数.
上的凸函数.
![]() 求实数a的取值范围;
求实数a的取值范围;
![]() 求函数
求函数![]() ,
,![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)![]() ;
;![]() 见解析
见解析
【解析】
![]() 求出函数的导数,解关于导函数的不等式,求出导函数的单调区间,从而判断函数的凹凸性即可;
求出函数的导数,解关于导函数的不等式,求出导函数的单调区间,从而判断函数的凹凸性即可;
![]() 求出函数的导数,问题转化为
求出函数的导数,问题转化为![]() 在
在![]() 上恒成立,求出a的范围即可;
上恒成立,求出a的范围即可;![]() 令
令![]() ,
,![]() ,则
,则![]() ,通过讨论a的范围,求出
,通过讨论a的范围,求出![]() 的最小值即可.
的最小值即可.
![]() 由
由![]() ,
,![]() ,
,
得![]() ,
,![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
故![]() ,
,
故对于![]() ,
,![]() ,
,
函数![]() 是定义域上的凸函数;
是定义域上的凸函数;
![]() 由
由![]() ,
,![]() ,
,
得![]() ,
,![]() ,
,
![]() 函数
函数![]() 是
是![]() 上的凸函数,
上的凸函数,
故![]() 在
在![]() 上恒成立,
上恒成立,
故![]() 在
在![]() 上恒成立,
上恒成立,
故![]() ,故
,故![]() ,
,
故实数a的范围是![]() ,
,
![]() 令
令![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
故F![]() ,
,
故H![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
![]() ;
;
![]() 当
当![]() 时,
时,![]() 在
在![]() 恒成立,
恒成立,
故F![]() 在
在![]() 递增,
递增,
故F![]() ,
,
故H![]() ;
;
![]() 当
当![]() 时,令
时,令![]() ,
,
![]() 存在零点
存在零点![]() ,
,![]() ,
,
其中![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
故![]() ,
,
结合![]() 的性质有:
的性质有:![]() 时,
时,![]() ,故F
,故F![]() ,
,
![]() 时,
时,![]() ,故F
,故F![]() ,
,
故F![]() 在
在![]() 上递减,在
上递减,在![]() 递增,
递增,
故F![]() ,
,
由![]() 知,
知,![]() ,
,
故![]() ,从而
,从而![]() ,
,
故F![]() ,
,
又![]() 的图象是一条不间断的曲线,
的图象是一条不间断的曲线,
故F![]() 在
在![]() 上有零点
上有零点![]() ,
,
故H![]() 的最小值是0,
的最小值是0,
综上,当![]() 时,
时,![]() 的最小值是
的最小值是![]() ,
,
当![]() 时,
时,![]() 的最小值是0,
的最小值是0,
当![]() 时,
时,![]() 的最小值是
的最小值是![]() .
.


科目:高中数学 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目,若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史科目的概率;
(Ⅲ)从选考方案确定的8名男生随机选出2名,设随机变量两名男生选考方案相同时![]() ,两名男生选考方案不同时
,两名男生选考方案不同时![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
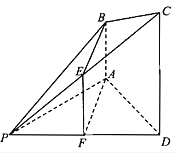
【题目】四棱锥![]() 中,已知
中,已知![]() 平面PAD,
平面PAD,![]() ,
,![]() ,E为棱PC上的一点,经过A,B,E三点的平面与棱PD相交于点F.
,E为棱PC上的一点,经过A,B,E三点的平面与棱PD相交于点F.
![]() 求证:
求证:![]() 平面PAD;
平面PAD;
![]() 求证:
求证:![]() ;
;
![]() 若平面
若平面![]() 平面PCD,求证:
平面PCD,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于项数为![]() (
(![]() )的有穷正整数数列
)的有穷正整数数列![]() ,记
,记![]() (
(![]() ),即
),即![]() 为
为![]() 中的最大值,称数列
中的最大值,称数列![]() 为数列
为数列![]() 的“创新数列”.比如
的“创新数列”.比如![]() 的“创新数列”为
的“创新数列”为![]() .
.
(1)若数列![]() 的“创新数列”
的“创新数列”![]() 为1,2,3,4,4,写出所有可能的数列
为1,2,3,4,4,写出所有可能的数列![]() ;
;
(2)设数列![]() 为数列
为数列![]() 的“创新数列”,满足
的“创新数列”,满足![]() (
(![]() ),求证:
),求证: ![]() (
(![]() );
);
(3)设数列![]() 为数列
为数列![]() 的“创新数列”,数列
的“创新数列”,数列![]() 中的项互不相等且所有项的和等于所有项的积,求出所有的数列
中的项互不相等且所有项的和等于所有项的积,求出所有的数列![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的金秋十月,越野e族阿拉善英雄会在内蒙古自治区阿拉善盟阿左旗腾格里沙漠举行,该项目已打造成集沙漠竞技运动、汽车文化极致体验、主题休闲度假为一体的超级汽车文化赛事娱乐综合体.为了减少对环境的污染,某环保部门租用了特制环保车清洁现场垃圾.通过查阅近5年英雄会参会人数![]() (万人)与沙漠中所需环保车辆数量
(万人)与沙漠中所需环保车辆数量![]() (辆),得到如下统计表:
(辆),得到如下统计表:
参会人数 | 11 | 9 | 8 | 10 | 12 |
所需环保车辆 | 28 | 23 | 20 | 25 | 29 |
(1)根据统计表所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知租用的环保车平均每辆的费用![]() (元)与数量
(元)与数量![]() (辆)的关系为
(辆)的关系为
![]() .主办方根据实际参会人数为所需要投入使用的环保车,
.主办方根据实际参会人数为所需要投入使用的环保车,
每辆支付费用6000元,超出实际需要的车辆,主办方不支付任何费用.预计本次英雄会大约有14万人参加,根据(Ⅰ)中求出的线性回归方程,预测环保部门在确保清洁任务完成的前提下,应租用多少辆环保车?获得的利润![]() 是多少?(注:利润
是多少?(注:利润![]() 主办方支付费用
主办方支付费用![]() 租用车辆的费用).
租用车辆的费用).
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
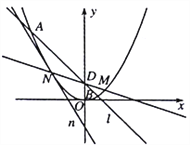
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在抛物线
在抛物线![]() :
: ![]() 上,直线
上,直线![]() :
: ![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点,且直线
两点,且直线![]() ,
, ![]() 的斜率之和为-1.
的斜率之和为-1.
(1)求![]() 和
和![]() 的值;
的值;
(2)若![]() ,设直线
,设直线![]() 与
与![]() 轴交于
轴交于![]() 点,延长
点,延长![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,记直线
,记直线![]() ,
, ![]() 与
与![]() 轴围成的三角形面积为
轴围成的三角形面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com