已知 (1-2x)7=a0+a1x+a2x2+…+a7x7;
求:(1)a0;
(2)a1+a2+…+a7;
(3)a1+a3+a5+a7.
解:(1)由二项式定理得:a
0=
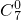
=1;
(2)∵(1-2x)
7=a
0+a
1x+a
2x
2+…+a
7x
7;
∴令x=1,得a
0+a
1+…+a
7=-1①,又a
0=1,
∴a
1+a
2+…+a
7=-1-1=-2;
(3)再令x=-1,得a
0-a
1+…-a
7=3
7②,①-②得:
2(a
1+a
3+a
5+a
7)=-1-3
7,
∴(a
1+a
3+a
5+a
7)=-

分析:(1)由二项式定理可知a
0=
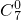
;
(2)令x=1,得a
0+a
1+…+a
7=-1①,结合a
0=1,即可求得a
1+a
2+…+a
7;
(3)令x=-1,得a
0-a
1+…-a
7=3
7②,①-②即可求得a
1+a
3+a
5+a
7.
点评:本题考查二项式定理的应用,着重考查赋值法与方程思想的应用,属于中档题.

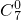 =1;
=1;
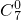 ;
;
