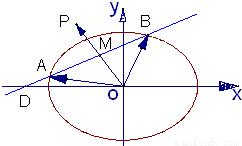
分析:(Ⅰ)当直线与x轴平行时,求得点P的坐标;设出直线l的方程及A,B,M,P的坐标,椭圆方程联立消去x,根据判别式大于0求得m的范围,进而根据韦达定理表示出y=y
1+y
2和x=x
1+x
2,进而联立消去m,即可求得P点的轨迹方程.
(Ⅱ)先看当l∥x轴时,A,B分别是椭圆长轴的两个端点,则点M在原点O处,求得|MD|,|MA|进而求得|
|的值;再看与x轴不平行时,根据弦长公式求得|MD|和|MA|的表达式,进而求得|
|的表达式,根据m的范围确定|
|的取值范围,最后综合可得答案.
解答:解:(Ⅰ)①若直线l∥x轴,则点P为(0,0);
②设直线l:x=my-2,
并设点A,B,M,P的坐标分别是A(x
1,y
1),B(x
2,y
2),M(x
0,y
0),P(x,y),
由
消去x,得(m
2+2)y
2-4my+2=0,①
由直线l与椭圆有两个不同的交点,可得△=(-4m)
2-8(m
2+2)>0,即8(m
2-2)>0,所以m
2>2
由
=
+
及方程①,得y=y
1+y
2=
,
x=x
1+x
2=(my
1-2)+(my
2-2)=-
,
即
由于m≠0(否则,直线l与椭圆无公共点),
将上方程组两式相除得,m=-
,代入到方程x=-
,
得x=-
,整理,得x
2+2y
2+4x=0(-2<x<0)
综上所述,点P的轨迹方程为x
2+2y
2+4x=0(-2<x<0)
(Ⅱ)①当l∥x轴时,A,B分别是椭圆长轴的两个端点,则点M在原点O处,
所以,|MD|=2,|MA|=
,所以,
=
②由方程①,得y
0=
=
,
|MD|=
|y
0-y
D|=
|MA|=|=
|y
0-y
1|=
=|=
=
=
m
2>2,-
∈(1,0),
∈(0,1),
∈[
,+∞)
点评:本题主要考查了直线与圆锥曲线的交点问题.常需要把直线与圆锥曲线的方程联立,利用韦达定理找打解决问题的突破扣.

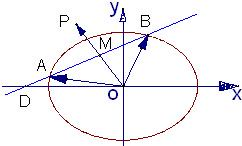 如图,已知过点D(-2,0)的直线l与椭圆
如图,已知过点D(-2,0)的直线l与椭圆

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案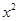 =2py(p>0)的切线l,切点A在第二象限.
=2py(p>0)的切线l,切点A在第二象限.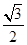 的椭圆
的椭圆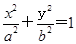 (a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
(a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
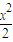 +y2=1交于不同的两点A、B,点M是弦AB的中点
+y2=1交于不同的两点A、B,点M是弦AB的中点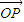 =
=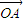 +
+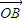 ,求点P的轨迹方程;
,求点P的轨迹方程;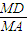 |的取值范围
|的取值范围