
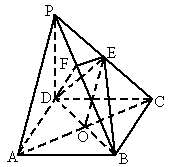
如图所示,在四棱锥PABCD中,底面ABC0是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明PA∥平面EDB;
(2)证明PB⊥平面EFD.
|
转化思想是立体几何中常用的数学思想,三种平行关系的转化垂直关系之间的转化等. 证明: (1)连结AC交BD于O,连结EO.∵底面 ABCD是正方形,∴ O点是AC的中点.在△PAC中,EO是中位线,∴ PA∥EO.而 EO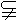 平面EDB,且PA 平面EDB,且PA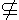 平面EDB, 平面EDB,
∴ PA∥平面EDB.(2) ∵PD⊥底面ABCD,且DC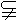 底面ABCD, 底面ABCD,
∴ PD⊥DC.∵ PD=DC,可知△PDC是等腰直角三角形,而 DE是斜边PC的中线,∴ DE⊥PC.①同理 PD⊥底面ABCD,得 PD⊥BC.∵底面ABCD是正方形,有DC⊥BC,∴ BC⊥平面PDC.而DE 平面PDC, 平面PDC,
∴ BC⊥DK.②由①②推得 DE⊥平面PBC.而 PB 平面PBC,∴DE⊥PB. 平面PBC,∴DE⊥PB.
又 EF⊥PB,且DE∩EF=E,∴ PB⊥平面EFD.一般地,线线关系或面面关系都转化为线面关系来分析解决,关系如下所示:
|


科目:高中数学 来源: 题型:
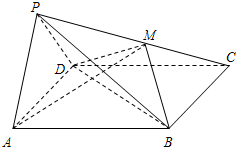 如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.
如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.查看答案和解析>>
科目:高中数学 来源: 题型:
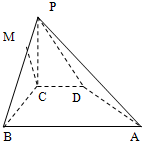 如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
(2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点.
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com