
【题目】已知函数![]() ,
, ![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的方程为
处的切线的方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
【答案】(1)a=﹣2;(2)[1,+∞)
【解析】试题分析:(1)由导数几何意义得![]() (2)化简不等式为
(2)化简不等式为![]() ,即
,即![]() 为单调递增函数,即
为单调递增函数,即![]() 恒成立,参变分离得
恒成立,参变分离得![]() 的最大值,即得实数
的最大值,即得实数![]() 的取值范围
的取值范围
试题解析:解:(1)y=f(x)﹣g(x)=![]() x2﹣alnx的导数为x﹣
x2﹣alnx的导数为x﹣![]() ,
,
曲线y=f(x)﹣g(x)在x=1处的切线斜率为k=1﹣a,
由切线的方程为6x﹣2y﹣5=0,可得1﹣a=3,
解得a=﹣2;
(2)h(x)=f(x)+g(x)=![]() x2+alnx,
x2+alnx,
对任意两个不等的正数x1,x2,都有![]() >2恒成立,即为
>2恒成立,即为
![]() >0,
>0,
令m(x)=h(x)﹣2x,可得m(x)在(0,+∞)递增,
由m′(x)=h′(x)﹣2=x+![]() ﹣2≥0恒成立,
﹣2≥0恒成立,
可得a≥x(2﹣x)的最大值,由x(2﹣x)=﹣(x﹣1)2+1可得最大值1,
则a≥1,即a的取值范围是[1,+∞)


科目:高中数学 来源: 题型:
【题目】O为原点的直角坐标系中,点A(4,﹣3)为△OAB的直角顶点,已知AB=2OA,且点B的纵坐标大于0
(1)求 ![]() 的坐标;
的坐标;
(2)求圆C1:x2﹣6x+y2+2y=0关于直线OB对称的圆C2的方程;在直线OB上是否存在点P,过点P的任意一条直线如果和圆C1圆C2都相交,则该直线被两圆截得的线段长相等,如果存在求出点P的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,设右焦点为
,设右焦点为![]() ,过原点
,过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 的中点为
的中点为![]() ,且
,且![]() .
.
(1)求弦![]() 的长;
的长;
(2)当直线![]() 的斜率
的斜率![]() ,且直线
,且直线![]() 时,
时, ![]() 交椭圆于
交椭圆于![]() ,若点
,若点![]() 在第一象限,求证:直线
在第一象限,求证:直线![]() 与
与![]() 轴围成一个等腰三角形.
轴围成一个等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校学生社团为了解“大数据时代”下大学生就业情况的满意度,对20名学生进行问卷计分调查(满分100分),得到如图所示的茎叶图:
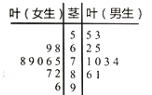
(1)计算男生打分的平均分,观察茎叶图,评价男女生打分的分散程度;
(2)从打分在80分以上的同学随机抽3人,求被抽到的女生人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)讨论![]() 的单调性;
的单调性;
(3)设过![]() 两点的直线的斜率为
两点的直线的斜率为![]() ,其中
,其中![]() 、
、![]() 为曲线
为曲线![]() 上的任意两点,并且
上的任意两点,并且![]() ,若
,若![]() 恒成立,证明:
恒成立,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O的方程为x2+y2=1,直线l1过点A(3,0),且与圆O相切.
(1)求直线l1的方程;
(2)设圆O与x轴相交于P,Q两点,M是圆O上异于P,Q的任意一点,过点A且与x轴垂直的直线为l2 , 直线PM交直线l2于点P′,直线QM交直线l2于点Q′.求证:以P′Q′为直径的圆C总经过定点,并求出定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将52名志愿者分成A,B两组参加义务植树活动,A组种植150捆白杨树苗,B组种植200捆沙棘树苗.假定A,B两组同时开始种植.
(1)根据历年统计,每名志愿者种植一捆白杨树苗用时![]() 小时,种植一捆沙棘树苗用时
小时,种植一捆沙棘树苗用时![]() 小时.应如何分配A,B两组的人数,使植树活动持续时间最短?
小时.应如何分配A,B两组的人数,使植树活动持续时间最短?
(2)在按(1)分配的人数种植1小时后发现,每名志愿者种植一捆白杨树苗用时仍为![]() 小时,而每名志愿者种植一捆沙棘树苗实际用时
小时,而每名志愿者种植一捆沙棘树苗实际用时![]() 小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.
小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直线坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为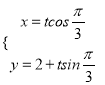 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的参数方程;
的参数方程;
(2)设点![]() 在
在![]() 上,
上, ![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com