
【题目】已知函数![]()
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若![]() 的解集包含
的解集包含![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) {x|x≤1,或x≥4};(2) -2≤a≤0.
【解析】试题分析:(1)根据绝对值定义将不等式转化为三个不等式组,最后求它们的并集(2)条件等价于f(x)≤|x-4|在[0,2]上恒成立,根据绝对值定义可得|x+a|≤2在[0,2]上恒成立,即得-2≤x+a≤2在[0,2]上恒成立,再根据函数最值可得![]() 的取值范围.
的取值范围.
试题解析:(1)当a=-3时,求不等式f(x)≥3,即|x-3|+|x-2|≥3,
|x+a|+|x-2|表示数轴上的x对应点到2、3对应点的距离之和,
而1和4对应点到2、3对应点的距离之和正好等于3,故|x-3|+|x-2|≥3的解集为{x|x≤1,或x≥4}.
(2)若f(x)≤|x-4|的解集包含[0,2],等价于f(x)≤|x-4|在[0,2]上恒成立,
即|x+a|≤4-x-|x-2|在[0,2]上恒成立,即|x+a|+2-x≤4-x在[0,2]上恒成立.
即|x+a|≤2在[0,2]上恒成立,即-2≤x+a≤2在[0,2]上恒成立,
即-2-x≤a≤2-x在[0,2]上恒成立,∴-2≤a≤0.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
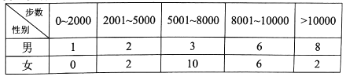
(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
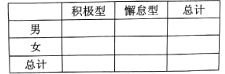
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附: 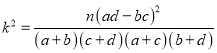 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算下列各式的值,写出必要的计算过程.
(1)0.064 ![]() ﹣(﹣
﹣(﹣ ![]() )0+16
)0+16 ![]() +0.25
+0.25 ![]()
(2)(log43+log83)(log32+log92)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆的中心在坐标原点,焦点在x轴上,A1 , A2 , B1 , B2为椭圆顶点,F2为右焦点,延长B1F2与A2B2交于点P,若∠B1PB2为钝角,则该椭圆离心率的取值范围是( ) 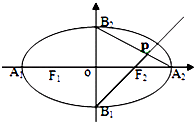
A.( ![]() ,1)
,1)
B.(0, ![]() )
)
C.(0, ![]() )
)
D.( ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定方程: ![]() ,则下列命题中:
,则下列命题中:
①该方程没有小于0的实数解;
②该方程有无数个实数解;
③该方程在(-∞,0)内有且只有一个实数解;
④若x0是该方程的实数解,则x0>-1.
正确的命题是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com