【答案】
分析:由已知中p:|x+1|>2和
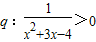
,我们可以求出满足条件p,q的参数x的范围,进而得到满足条件¬p,¬q的参数x的范围,结合参数x的范围分别讨论¬p⇒¬q与¬q⇒¬p的真假,进而根据充要条件的定义即可得到答案.
解答:解:由命题p得:x>1或x<-3;由命题q得:x>1或x<-4
则¬p为:-3≤x≤1;¬q为:-4≤x≤1
可知:¬p⇒¬q反之则不成立.
所以¬p是¬q的充分不必要条件.
点评:本题考查的知识点是必要条件,充分条件与充要条件的判断,其中解绝对值不等式和分式不等式求出满足条件p,q的参数x的范围,进而得到满足条件¬p,¬q的参数x的范围,是解答本题的关键.

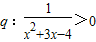 ,试问¬p是¬q的什么条件?
,试问¬p是¬q的什么条件?