Question

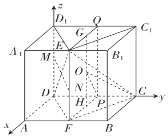
【题目】在正方体中，分别为线段的中点，为四棱锥的外接球的球心，点分别是直线上的动点，记直线与所成角为，则当最小时，（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

如图，设分别为棱和的中点，则四棱锥的外接球即三棱柱的外接球，所以其外接球球心为上、下底面三角形外心和连线的中点，是平面内的一条动直线，所以的最小值是直线与平面所成角，即问题转化为求直线与平面所成角的正切值，通过建立空间直角坐标算出直线与平面所成角的正切值即可.

如图，设分别为棱和的中点，

则四棱锥的外接球即三棱柱的外接球，

因为三棱柱为直三棱柱，

所以其外接球球心为上、下底面三角形外心和连线的中点.

由题意，是平面内的一条动直线，所以的最小值是直线与平面所成角，即问题转化为求直线与平面所成角的正切值.

不妨设正方体的棱长为2，则.

因为为等腰三角形，所以外接圆的直径为，

则，从而.

如图，以为原点，以的方向为轴，轴，轴的正方向建立空间直角坐标系，

则，，，，，

，

设平面的一个法向量为，

则，令，则，

因为，所以，则.

故选：D