
【题目】已知函数![]() 的图象在
的图象在![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求![]() 的值;
的值;
(2)若函数![]() ,讨论
,讨论![]() 的单调性与极值;
的单调性与极值;
(3)证明:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() 单调递减区间为
单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,
,![]() 的极小值为
的极小值为![]() ,无极大值;(3)见解析.
,无极大值;(3)见解析.
【解析】
(1)切点既在切线上又在曲线上得一方程,再根据斜率等于该点的导数再列一方程,解方程组即可;
(2)先对![]() 求导数,根据导数判断和求解即可.
求导数,根据导数判断和求解即可.
(3)把证明![]() 转化为证明
转化为证明![]() ,然后证明
,然后证明![]() 极小值大于
极小值大于![]() 极大值即可.
极大值即可.
解:(1)函数![]() 的定义域为
的定义域为![]()
由已知得![]() ,则
,则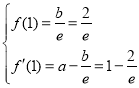 ,解得
,解得![]() .
.
(2)由题意得![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,所以
,所以![]() 单调递增,
单调递增,
所以,![]() 单调递减区间为
单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,
,
![]() 的极小值为
的极小值为![]() ,无极大值.
,无极大值.
(3)要证![]() 成立,
成立,
只需证![]() 成立.
成立.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() 单调递减,
单调递减,
所以![]() 的极大值为
的极大值为![]() ,即
,即![]()
由(2)知,![]() 时,
时,![]() ,且
,且![]() 的最小值点与
的最小值点与![]() 的最大值点不同,所以
的最大值点不同,所以![]() ,即
,即![]() .
.
所以,![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】为检验![]() 两条生产线的优品率,现从两条生产线上各抽取
两条生产线的优品率,现从两条生产线上各抽取![]() 件产品进行检测评分,用茎叶图的形式记录,并规定高于
件产品进行检测评分,用茎叶图的形式记录,并规定高于![]() 分为优品.前
分为优品.前![]() 件的评分记录如下,第
件的评分记录如下,第![]() 件暂不公布.
件暂不公布.

(1)求所抽取的![]() 生产线上的
生产线上的![]() 个产品的总分小于
个产品的总分小于![]() 生产线上的第
生产线上的第![]() 个产品的总分的概率;
个产品的总分的概率;
(2)已知![]() 生产线的第
生产线的第![]() 件产品的评分分别为
件产品的评分分别为![]() .
.
①从![]() 生产线的
生产线的![]() 件产品里面随机抽取
件产品里面随机抽取![]() 件,设非优品的件数为
件,设非优品的件数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
②以所抽取的样本优品率来估计![]() 生产线的优品率,从
生产线的优品率,从![]() 生产线上随机抽取
生产线上随机抽取![]() 件产品,记优品的件数为
件产品,记优品的件数为![]() ,求
,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
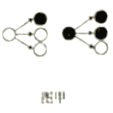
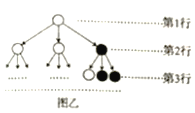
【题目】分形几何学是数学家伯努瓦·曼得尔布罗在20世纪70年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图甲所示的分形规律可得如图乙所示的一个树形图:记图乙中第![]() 行黑圈的个数为
行黑圈的个数为![]() ,则(1)
,则(1)![]() _______;(2)
_______;(2)![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民收入逐年增长.某地区2014年至2018年农村居民家庭人均纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
人均纯收入 | 5 | 4 | 7 | 8 | 10 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2014年至2018年该地区农村居民家庭人均纯收入的变化情况,并预测2019年该地区农村居民家庭人均纯收入为多少?
附:回归直线的斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》 是我国古代的天文学和数学著作。其中一个问题的大意为:一年有二十四个节气(如图),每个节气晷长损益相同(即物体在太阳的照射下影子长度的增加量和减少量相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:ー丈等于十尺,一尺等于十寸),则立冬节气的晷长为( )
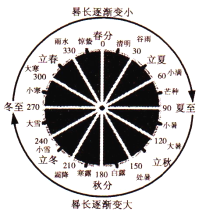
A. 九尺五寸 B. 一丈五寸 C. 一丈一尺五寸 D. 一丈六尺五寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com