Question

【题目】已知函数．

（1）若函数在上单调递增，求实数的值；

（2）定义：若直线与曲线都相切，我们称直线为曲线、的公切线，证明：曲线与总存在公切线．

Answer 1

【答案】（1）；（2）见解析.

【解析】

（1）求出导数，问题转化为在上恒成立，利用导数求出的最小值即可求解；

（2）分别设切点横坐标为，利用导数的几何意义写出切线方程，问题转化为证明两直线重合，只需满足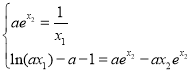有解即可，利用函数的导数及零点存在性定理即可证明存在.

（1），

函数在上单调递增等价于在上恒成立．

令，得，

所以在单调递减，在单调递增，则．

因为，则在上恒成立等价于在上恒成立；

又

，

所以，即．

（2）设的切点横坐标为，则

切线方程为……①

设的切点横坐标为，则，

切线方程为……②

若存在，使①②成为同一条直线，则曲线与存在公切线，由①②得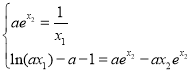消去得

即

令，则

所以，函数在区间上单调递增，

，使得

时总有

又时，

在上总有解

综上，函数与总存在公切线．