练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某市移动公司为了提高服务质量，决定对使用A，B两种套餐的集团用户进行调查，准备从本市个人数超过1000人的大集团和8个人数低于200人的小集团中随机抽取若干个集团进行调查，若一次抽取2个集团，全是小集团的概率为．

    求n的值；

    若取出的2个集团是同一类集团，求全为大集团的概率；

    若一次抽取4个集团，假设取出小集团的个数为X，求X的分布列和期望．

    【答案】（1）；（2）；（3）详见解析.

    【解析】

    （1）由题意根据全是小集团的概率列方程求出的值；

    （2）根据古典概型的概率公式计算全为大集团的概率值；

    （3）由题意知随机变量的可能取值，计算对应的概率值，写出分布列，求出数学期望值．

    （1）由题意知共有个集团，取出2个集团的方法总数是，其中全是小集团的情况有，故全是小集团的概率是，

    整理得到即，解得．

    （2）若2个全是大集团，共有种情况；

    若2个全是小集团，共有种情况；

    故全为大集团的概率为．

    （3）由题意知，随机变量的可能取值为，

    计算，，，

    ，，

    ；

    故的分布列为：

    0

    1

    2

    3

    4

    数学期望为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）若函数在上单调递增，求实数的值；

    （2）定义：若直线与曲线都相切，我们称直线为曲线、的公切线，证明：曲线与总存在公切线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】出版商为了解某科普书一个季度的销售量（单位：千本）和利润（单位：元/本）之间的关系，对近年来几次调价之后的季销售量进行统计分析，得到如下的10组数据.

    序号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    2.4

    3.1

    4.6

    5.3

    6.4

    7.1

    7.8

    8.8

    9.5

    10

    18.1

    14.1

    9.1

    7.1

    4.8

    3.8

    3.2

    2.3

    2.1

    1.4

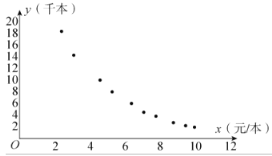
    根据上述数据画出如图所示的散点图：

    （1）根据图中所示的散点图判断和哪个更适宜作为销售量关于利润的回归方程类型？（给出判断即可，不需要说明理由）

    （2）根据（1）中的判断结果及参考数据，求出关于的回归方程；

    （3）根据回归方程设该科普书一个季度的利润总额为（单位：千元），当季销售量为何值时，该书一个季度的利润总额预报值最大？（季利润总额=季销售量×每本书的利润）

    参考公式及参考数据：

    ①对于一组数据，其回归直线的斜率和截距的公式分别为.

    ②参考数据：

    6.50

    6.60

    1.75

    82.50

    2.70

    表中.另：.计算时，所有的小数都精确到0.01.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市对所有高校学生进行普通话水平测试，发现成绩服从正态分布N（μ，σ2），下表用茎叶图列举出来抽样出的10名学生的成绩．

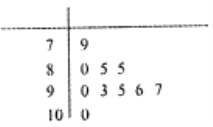
    （1）计算这10名学生的成绩的均值和方差；

    （2）给出正态分布的数据：P（μ﹣σ＜X＜μ+σ）=0.6826，P（μ﹣2σ＜X＜μ+2σ）=0.9544．

    由（1）估计从全市随机抽取一名学生的成绩在（76，97）的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】青岛二中学生民议会在周五下午高峰时段，对公交路甲站和线乙站各随机抽取了位乘客，统计其乘车等待时间（指乘客从等车到乘上车的时间，乘车等待时间不超过分钟）.将统计数据按，，，…，分组，制成频率分布直方图：

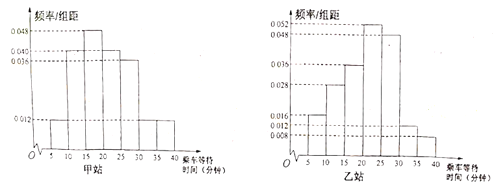
    假设乘客乘车等待时间相互独立.

    （1）此时段，从甲站的乘客中随机抽取人，记为事件；从乙站的乘客中随机抽取人，记为事件.若用频率估计概率，求“两人乘车等待时间都小于分钟”的概率；

    （2）此时段，从乙站的乘客中随机抽取人（不重复抽取），抽得在的人数为，求随机变量的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数且.

    （1）求实数的值；

    （2）令在上的最小值为，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对某两名高三学生连续9次数学测试的成绩（单位：分）进行统计得到如下折线图.下列有关这两名学生数学成绩的分析中，正确的结论是（ ）

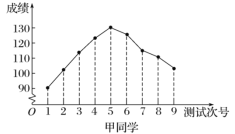
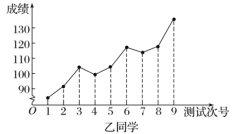
    A.甲同学的成绩折线图具有较好的对称性，与正态曲线相近，故而平均成绩为130分

    B.根据甲同学成绩折线图中的数据进行统计，估计该同学平均成绩在区间内

    C.乙同学的数学成绩与测试次号具有比较明显的线性相关性，且为正相关

    D.乙同学在这连续九次测验中的最高分与最低分的差超过40分

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中为真命题的是(　　)

    A.命题“若，则”的否命题

    B.命题“若x＞y，则x＞|y|”的逆命题

    C.命题“若x＝1，则”的否命题

    D.命题“已知，若，则a＞b”的逆命题、否命题、逆否命题均为真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】按照下列要求，分别求有多少种不同的方法？

    （1）5个不同的小球放入3个不同的盒子；

    （2）5个不同的小球放入3个不同的盒子，每个盒子至少一个小球；

    （3）5个相同的小球放入3个不同的盒子，每个盒子至少一个小球；

    （4）5个不同的小球放入3个不同的盒子，恰有1个空盒．

    查看答案和解析>>

    同步练习册答案