Question

【题目】青岛二中学生民议会在周五下午高峰时段，对公交路甲站和线乙站各随机抽取了位乘客，统计其乘车等待时间（指乘客从等车到乘上车的时间，乘车等待时间不超过分钟）.将统计数据按，，，…，分组，制成频率分布直方图：

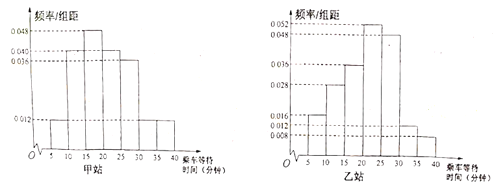
假设乘客乘车等待时间相互独立.

（1）此时段，从甲站的乘客中随机抽取人，记为事件；从乙站的乘客中随机抽取人，记为事件.若用频率估计概率，求“两人乘车等待时间都小于分钟”的概率；

（2）此时段，从乙站的乘客中随机抽取人（不重复抽取），抽得在的人数为，求随机变量的分布列与数学期望.

Answer 1

【答案】（1）.（2）分布列见解析，期望为.

【解析】

（1）由设表示事件“乘客乘车等待时间都小于分钟”，表示“乘客乘车等待时间都小于分钟”，表示“乘客乘车等待时间都小于分钟”，求得，，结合题意，即可求得答案.

（2）的所有可能取值为：，求出相应的概率，即可得到的分布列数学期望．即可求得答案.

（1）设表示事件“乘客乘车等待时间都小于分钟”，表示“乘客乘车等待时间都小于分钟”，

表示“乘客乘车等待时间都小于分钟”，

由题意得：

“乘客，乘车等待时间都小于分钟”的概率：

（2）从乙站的乘客中和人数比例为：

随机抽取人（不重复抽取），

抽得在的人X的可能取值为，且

的分布列为：

	1	2	3	4