练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥中，侧面为等边三角形，且垂直于底面， ，分别是的中点.

    （1）证明：平面平面；

    （2）已知点在棱上且，求直线与平面所成角的余弦值.

    【答案】（1）证明见解析；（2）.

    【解析】

    （1）由平面几何知识可得出四边形是平行四边形，可得面，再由面面平行的判定可证得面面平行；

    （2）由（1）可知，两两垂直，故建立空间直角坐标系，可求得面PAB的法向量，再运用线面角的向量求法，可求得直线与平面所成角的余弦值.

    （1），,又，，,

    而、分别是、的中点，， 故面,

    又且，故四边形是平行四边形,面,

    又，是面内的两条相交直线, 故面面.

    （2）由（1）可知，两两垂直，故建系如图所示,则

    ，

    ，，,

    设是平面PAB的法向量,，

    令，则,,

    直线NE与平面所成角的余弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】青岛二中学生民议会在周五下午高峰时段，对公交路甲站和线乙站各随机抽取了位乘客，统计其乘车等待时间（指乘客从等车到乘上车的时间，乘车等待时间不超过分钟）.将统计数据按，，，…，分组，制成频率分布直方图：

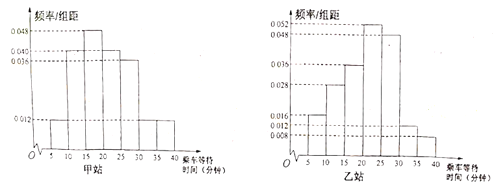
    假设乘客乘车等待时间相互独立.

    （1）此时段，从甲站的乘客中随机抽取人，记为事件；从乙站的乘客中随机抽取人，记为事件.若用频率估计概率，求“两人乘车等待时间都小于分钟”的概率；

    （2）此时段，从乙站的乘客中随机抽取人（不重复抽取），抽得在的人数为，求随机变量的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）如图所示，是一个矩形花坛，其中米，米．现将矩形花坛扩建成一个更大的矩形花坛，要求：在上，在上，对角线过点，且矩形的面积小于150平方米．

    （1）设长为米，矩形的面积为平方米，试用解析式将表示成的函数，并确定函数的定义域；

    （2）当的长度是多少时，矩形的面积最小？并求最小面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：指数函数在R上是单调减函数；命题q：关于x的方程有实根，

    （1）若p为真，求a的范围

    （2）若q为真，求的范围

    （3）若p或q为真，p且q为假，求实数a的范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校艺术节对四件参赛作品只评一件一等奖，在评奖揭晓前，甲，乙，丙，丁四位同学对这四件参赛作品预测如下：

    甲说：“是或作品获得一等奖”； 乙说：“ 作品获得一等奖”；

    丙说：“ 两件作品未获得一等奖”； 丁说：“是作品获得一等奖”．

    评奖揭晓后，发现这四位同学中只有两位说的话是对的，则获得一等奖的作品是_________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】按照下列要求，分别求有多少种不同的方法？

    （1）5个不同的小球放入3个不同的盒子；

    （2）5个不同的小球放入3个不同的盒子，每个盒子至少一个小球；

    （3）5个相同的小球放入3个不同的盒子，每个盒子至少一个小球；

    （4）5个不同的小球放入3个不同的盒子，恰有1个空盒．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求函数的图象在处的切线方程；

    （2）讨论函数的单调性；

    （3）当时，若方程有两个不相等的实数根，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若在上单调递增，求实数的取值范围；

    （2）设，若，恒有成立，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数(为常数)，曲线在与轴的交点A处的切线与轴平行．

    (1)求的值及函数的单调区间；

    (2)若存在不相等的实数使成立，试比较与的大小．

    查看答案和解析>>

    同步练习册答案