
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,若
,若![]() ,恒有
,恒有![]() 成立,求
成立,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由![]() 在
在![]() 上单调递增,可得
上单调递增,可得![]() 在
在![]() 上恒成立,利用分离参数法求出
上恒成立,利用分离参数法求出![]() 的范围即可;
的范围即可;
(2)设![]() ,
,![]() ,根据条件求出
,根据条件求出![]() 的范围后,根据
的范围后,根据![]() ,可得
,可得![]() 的最小值.
的最小值.
解:(1)由![]() ,得
,得![]() ,
,
由![]() 在
在![]() 上单调递增,可得
上单调递增,可得![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
当![]() 时,
时,![]() ;当
;当![]() ,则
,则![]() ,∴
,∴![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() .
.
(2)设![]() ,
,![]() ,
,
则![]() .
.
设![]() ,则
,则![]() ,
,
∴![]() 单调递增,即
单调递增,即![]() 在
在![]() 上单调递增,
上单调递增,
∴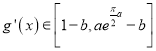 .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,不符合题意;
,不符合题意;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,![]() ,符合题意;
,符合题意;
当![]() 时,由于
时,由于![]() 为一个单调递增的函数,
为一个单调递增的函数,
而![]() ,
,![]() ,
,
由零点存在性定理,必存在一个零点![]() ,使得
,使得![]() ,
,
从而![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
因此只需![]() ,∴
,∴![]() ,
,
∴![]() ,从而
,从而![]() ,
,
综上,![]() 的取值范围为
的取值范围为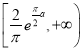 ,
,
因此![]() .
.
设![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
从而![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 为等边三角形,且垂直于底面
为等边三角形,且垂直于底面![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)已知点![]() 在棱
在棱![]() 上且
上且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学习强国活动中,某市图书馆的科技类图书和时政类图书是市民借阅的热门图书.为了丰富图书资源,现对已借阅了科技类图书的市民(以下简称为“问卷市民”)进行随机问卷调查,若不借阅时政类图书记1分,若借阅时政类图书记2分,每位市民选择是否借阅时政类图书的概率均为![]() ,市民之间选择意愿相互独立.
,市民之间选择意愿相互独立.
(1)从问卷市民中随机抽取4人,记总得分为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)(i)若从问卷市民中随机抽取![]() 人,记总分恰为
人,记总分恰为![]() 分的概率为
分的概率为![]() ,求数列
,求数列![]() 的前10项和;
的前10项和;
(ⅱ)在对所有问卷市民进行随机问卷调查过程中,记已调查过的累计得分恰为![]() 分的概率为
分的概率为![]() (比如:
(比如:![]() 表示累计得分为1分的概率,
表示累计得分为1分的概率,![]() 表示累计得分为2分的概率,
表示累计得分为2分的概率,![]() ),试探求
),试探求![]() 与
与![]() 之间的关系,并求数列
之间的关系,并求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
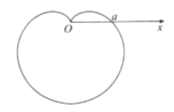
【题目】据说,年过半百的笛卡尔担任瑞典一小公国的公主克里斯蒂娜的数学老师,日久生情,彼此爱慕,其父国王知情后大怒,将笛卡尔流放回法国,并软禁公主,笛卡尔回法国后染上黑死病,连连给公主写信,死前最后一封信只有一个公式:![]()
![]() 国王不懂,将这封信交给了公主,公主用笛卡尔教她的坐标知识,画出了这个图形“心形线”.明白了笛卡尔的心意,登上了国王宝座后,派人去寻笛卡尔,其逝久矣(仅是一个传说).心形线是由一个圆上的一个定点,当该圆绕着与其相切且半径相同的另外一个圆周上滚动时,这个定点的轨迹,因其形状像心形而得名.在极坐标系
国王不懂,将这封信交给了公主,公主用笛卡尔教她的坐标知识,画出了这个图形“心形线”.明白了笛卡尔的心意,登上了国王宝座后,派人去寻笛卡尔,其逝久矣(仅是一个传说).心形线是由一个圆上的一个定点,当该圆绕着与其相切且半径相同的另外一个圆周上滚动时,这个定点的轨迹,因其形状像心形而得名.在极坐标系![]() 中,方程
中,方程![]()
![]() 表示的曲线
表示的曲线![]() 就是一条心形线,如图,以极轴
就是一条心形线,如图,以极轴![]() 所在直线为
所在直线为![]() 轴,极点
轴,极点![]() 为坐标原点的直角坐标系
为坐标原点的直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为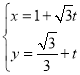 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若曲线![]() 与
与![]() 相交于
相交于![]() 、
、![]() 、
、![]() 三点,求线段
三点,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日是全国爱牙日,为了迎接这一节日,某地区卫生部门成立了调查小组,调查“常吃零食与患龋齿的关系”,对该地区小学六年级
日是全国爱牙日,为了迎接这一节日,某地区卫生部门成立了调查小组,调查“常吃零食与患龋齿的关系”,对该地区小学六年级![]() 名学生进行检查,按患龋齿的不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有
名学生进行检查,按患龋齿的不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有![]() 名,常吃零食但不患龋齿的学生有
名,常吃零食但不患龋齿的学生有![]() 名,不常吃零食但患齲齿的学生有
名,不常吃零食但患齲齿的学生有![]() 名.
名.
(1)完成答卷中的![]() 列联表,问:能否在犯错率不超过
列联表,问:能否在犯错率不超过![]() 的前提下,认为该地区学生的常吃零食与患龋齿有关系?
的前提下,认为该地区学生的常吃零食与患龋齿有关系?
(2)![]() 名区卫生部门的工作人员随机分成两组,每组
名区卫生部门的工作人员随机分成两组,每组![]() 人,一组负责数据收集,另一组负责数据处理,求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
人,一组负责数据收集,另一组负责数据处理,求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
附: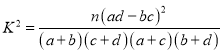
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
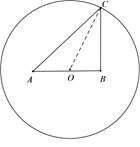
【题目】某公园准备在一圆形水池里设置两个观景喷泉,观景喷泉的示意图如图所示,![]() 两点为喷泉,圆心
两点为喷泉,圆心![]() 为
为![]() 的中点,其中
的中点,其中![]() 米,半径
米,半径![]() 米,市民可位于水池边缘任意一点
米,市民可位于水池边缘任意一点![]() 处观赏.
处观赏.
(1)若当![]() 时,
时,![]() ,求此时
,求此时![]() 的值;
的值;
(2)设![]() ,且
,且![]() .
.
(i)试将![]() 表示为
表示为![]() 的函数,并求出
的函数,并求出![]() 的取值范围;
的取值范围;
(ii)若同时要求市民在水池边缘任意一点![]() 处观赏喷泉时,观赏角度
处观赏喷泉时,观赏角度![]() 的最大值不小于
的最大值不小于![]() ,试求
,试求![]() 两处喷泉间距离的最小值.
两处喷泉间距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为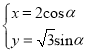 (
(![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换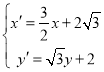 得到曲线
得到曲线![]() ,以原点为极点、
,以原点为极点、![]() 轴的正半轴为极轴,建立极坐标系.
轴的正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曾玉、刘云、李梦、张熙四人被北京大学、清华大学、武汉大学和复旦大学录取,他们分别被哪个学校录取,同学们做了如下的猜想
甲同学猜:曾玉被武汉大学录取,李梦被复旦大学录取
同学乙猜:刘云被清华大学录取,张熙被北京大学录取
同学丙猜:曾玉被复旦大学录取,李梦被清华大学录取
同学丁猜:刘云被清华大学录取,张熙被武汉大学录取
结果,恰好有三位同学的猜想各对了一半,还有一位同学的猜想都不对
那么曾玉、刘云、李梦、张熙四人被录取的大小可能是( )
A.北京大学、清华大学、复旦大学、武汉大学
B.武汉大学、清华大学、复旦大学、北京大学
C.清华大学、北京大学、武汉大学 、复旦大学
D.武汉大学、复旦大学、清华大学、北京大学
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com