
【题目】按照下列要求,分别求有多少种不同的方法?
(1)5个不同的小球放入3个不同的盒子;
(2)5个不同的小球放入3个不同的盒子,每个盒子至少一个小球;
(3)5个相同的小球放入3个不同的盒子,每个盒子至少一个小球;
(4)5个不同的小球放入3个不同的盒子,恰有1个空盒.
【答案】(1)243种(2)150种(3)6种(4)90种
【解析】
(1)利用分步乘法计数原理可求;
(2)先把5个小球分为三组,然后再放入三个盒中可得;
(3)利用隔板法进行求解,5个相同的小球,分成3组共有![]() 种方法;
种方法;
(4)先把5个小球分为两组,然后再放入三个盒中可得.
(1)5个不同的小球放入3个不同的盒子,每个小球都有3种可能,利用乘法原理可得不同的方法有![]() ;
;
(2)5个不同的小球放入3个不同的盒子,每个盒子至少一个小球,先把5个小球分组,有两种分法:2、2、1;3、1、1;再放入3个不同的盒子,故不同的方法共有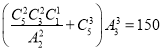 ;
;
(3)5个相同的小球放入3个不同的盒子,每个盒子至少一个小球,类似于在5个小球间的空隙中,放入2个隔板,把小球分为3组,故不同的方法共有![]() ;
;
(4)5个不同的小球放入3个不同的盒子,恰有一个空盒,先把5个小球分2组,有两种分法:3、2、0;4、1、0;再放入3个不同的盒子,故不同的方法共有![]() .
.


科目:高中数学 来源: 题型:
【题目】某市移动公司为了提高服务质量,决定对使用A,B两种套餐的集团用户进行调查,准备从本市![]() 个人数超过1000人的大集团和8个人数低于200人的小集团中随机抽取若干个集团进行调查,若一次抽取2个集团,全是小集团的概率为
个人数超过1000人的大集团和8个人数低于200人的小集团中随机抽取若干个集团进行调查,若一次抽取2个集团,全是小集团的概率为![]() .
.
![]() 求n的值;
求n的值;
![]() 若取出的2个集团是同一类集团,求全为大集团的概率;
若取出的2个集团是同一类集团,求全为大集团的概率;
![]() 若一次抽取4个集团,假设取出小集团的个数为X,求X的分布列和期望.
若一次抽取4个集团,假设取出小集团的个数为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项和.
项和.
(1)若数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,求数列
的等比数列,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)在(2)的条件下,设![]() ,求证:数列
,求证:数列![]() 中的任意一项总可以表示成该数列其他两项之积.
中的任意一项总可以表示成该数列其他两项之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大时,点P的坐标.
的距离的最大时,点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 为等边三角形,且垂直于底面
为等边三角形,且垂直于底面![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)已知点![]() 在棱
在棱![]() 上且
上且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃.下面叙述不正确的是 ( )

A. 各月的平均最低气温都在0℃以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于20℃的月份有5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在学习强国活动中,某市图书馆的科技类图书和时政类图书是市民借阅的热门图书.为了丰富图书资源,现对已借阅了科技类图书的市民(以下简称为“问卷市民”)进行随机问卷调查,若不借阅时政类图书记1分,若借阅时政类图书记2分,每位市民选择是否借阅时政类图书的概率均为![]() ,市民之间选择意愿相互独立.
,市民之间选择意愿相互独立.
(1)从问卷市民中随机抽取4人,记总得分为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)(i)若从问卷市民中随机抽取![]() 人,记总分恰为
人,记总分恰为![]() 分的概率为
分的概率为![]() ,求数列
,求数列![]() 的前10项和;
的前10项和;
(ⅱ)在对所有问卷市民进行随机问卷调查过程中,记已调查过的累计得分恰为![]() 分的概率为
分的概率为![]() (比如:
(比如:![]() 表示累计得分为1分的概率,
表示累计得分为1分的概率,![]() 表示累计得分为2分的概率,
表示累计得分为2分的概率,![]() ),试探求
),试探求![]() 与
与![]() 之间的关系,并求数列
之间的关系,并求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日是全国爱牙日,为了迎接这一节日,某地区卫生部门成立了调查小组,调查“常吃零食与患龋齿的关系”,对该地区小学六年级
日是全国爱牙日,为了迎接这一节日,某地区卫生部门成立了调查小组,调查“常吃零食与患龋齿的关系”,对该地区小学六年级![]() 名学生进行检查,按患龋齿的不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有
名学生进行检查,按患龋齿的不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有![]() 名,常吃零食但不患龋齿的学生有
名,常吃零食但不患龋齿的学生有![]() 名,不常吃零食但患齲齿的学生有
名,不常吃零食但患齲齿的学生有![]() 名.
名.
(1)完成答卷中的![]() 列联表,问:能否在犯错率不超过
列联表,问:能否在犯错率不超过![]() 的前提下,认为该地区学生的常吃零食与患龋齿有关系?
的前提下,认为该地区学生的常吃零食与患龋齿有关系?
(2)![]() 名区卫生部门的工作人员随机分成两组,每组
名区卫生部门的工作人员随机分成两组,每组![]() 人,一组负责数据收集,另一组负责数据处理,求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
人,一组负责数据收集,另一组负责数据处理,求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
附: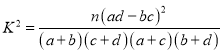
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com