Question

设{lga_n}成等差数列，公差d=lg3，且{lga_n}的前三项和为6lg3，则{a_n}的通项为    ．

Answer 1

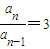
【答案】分析：由题意可得，lga_n-lga_n-1=lg3，即，从而可得{a_n}是以3为公比的等比数列，由{lga_n}的前三项和为6lg3，结合a_n＞0可求a₂=9，代入等比数列的通项可求
解答：解：由题意可得，lga_n-lga_n-1=lg3
∴
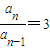
∴{a_n}是以3为公比的等比数列
∵lga₁+lga₂+lga₃=lg（a₁a₂a₃）=6lg3
∴
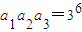
由等比数列的性质可得，
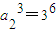
∵a_n＞0
∴a₂=9，a₁=3
∴
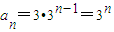
故答案为：
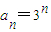点评：本题主要考查了对数的基本运算性质的应用，等比数列的性质及通项公式的应用