
分析 根据所给的带有绝对值的函数式,讨论去掉绝对值,得到一个分段函数,利用二次函数的单调性即可得到减区间.
解答 解:当x>-2时,f(x)=x2+2x,
当x≤-2时,f(x)=-x2-2x,
这样就得到一个分段函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x>-2}\\{{-x}^{2}-2x,x≤-2}\end{array}\right.$.
f(x)=x2+2x的对称轴为:x=-1,开口向上,x>-2时是增函数;
f(x)=-x2-2x,开口向下,对称轴为x=-1,
则x<-1时函数是增函数,-2<x<-1时函数是减函数.
即有函数的单调减区间是[-2,-1].
故答案为:[-2,-1].
点评 本题考查二次函数的性质,本题解题的关键是去掉绝对值,把函数化成基本初等函数,可以通过函数的性质或者图象得到结果.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:解答题
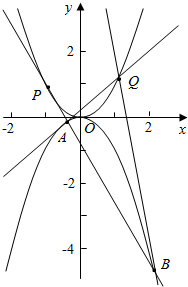 如图,过抛物线${C_1}:{x^2}=2py$上的一点Q与抛物线${C_2}:{x^2}=-2py$相切于A,B两点.若抛物线${C_1}:{x^2}=2py$的焦点F1到抛物线${C_2}:{x^2}=-2py$的焦点F2的距离为$\frac{1}{2}$
如图,过抛物线${C_1}:{x^2}=2py$上的一点Q与抛物线${C_2}:{x^2}=-2py$相切于A,B两点.若抛物线${C_1}:{x^2}=2py$的焦点F1到抛物线${C_2}:{x^2}=-2py$的焦点F2的距离为$\frac{1}{2}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$或$\frac{π}{2}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com