
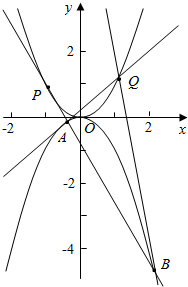
 如图,过抛物线${C_1}:{x^2}=2py$上的一点Q与抛物线${C_2}:{x^2}=-2py$相切于A,B两点.若抛物线${C_1}:{x^2}=2py$的焦点F1到抛物线${C_2}:{x^2}=-2py$的焦点F2的距离为$\frac{1}{2}$
如图,过抛物线${C_1}:{x^2}=2py$上的一点Q与抛物线${C_2}:{x^2}=-2py$相切于A,B两点.若抛物线${C_1}:{x^2}=2py$的焦点F1到抛物线${C_2}:{x^2}=-2py$的焦点F2的距离为$\frac{1}{2}$分析 (Ⅰ)确定抛物线的焦点坐标,即可求抛物线C1的方程;
(Ⅱ)求出直线AQ的方程、BQ的方程,AB的方程,即可证明直线AB与抛物线C1相切于一点P.
解答 (I)解:设抛物线C1的焦点坐标为${F_1}(0,\frac{p}{2})$,…(2分)
抛物线C2的焦点坐标为${F_2}(0,-\frac{p}{2})$…(4分)
则$|{F_1}{F_2}|=p=\frac{1}{2}$…(5分)
所以抛物线C1的方程为:y=x2.…(6分)
(II)证明:设点$Q({x_0},x_0^2)$,$A({x_1},-x_1^2),B({x_2},-x_2^2)$
切线AQ的方程是:$y+x_1^2={k_1}(x-{x_1})$,因为AQ与抛物线${C_1}:y={x^2}$相切,
则${x^2}+{k_1}x-{k_1}{x_1}-x_1^2=0$,
则${△_1}=k_1^2+4{k_1}{x_1}+4x_1^2=0$,则k1=-2x1,…(8分)
∴直线AQ的方程是:$y=-2{x_1}x+x_1^2$,
同理BQ的方程是:$y=-2{x_2}x+x_2^2$.…(9分)
联立可以得到:$\left\{\begin{array}{l}{x_1}+{x_2}=2{x_0}\\{x_1}{x_2}=-x_0^2\end{array}\right.$.…(11分)
而直线AB的方程是:y=-(x1+x2)x+x1x2,即$y=-2{x_0}x-x_0^2$,…(13分)
联立${C_1}:y={x^2}$,可以得到:${x^2}+2{x_0}x+x_0^2=0$,${△_2}=4x_0^2-4x_0^2=0$,
则直线AB与抛物线${C_1}:y={x^2}$相切.…(15分)
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 110 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 1.323 | 2.072 | 2.706 | 3.845 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | λ∈(0,1) | B. | λ∈(1,2) | C. | λ∈(2,3) | D. | λ∈(3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在0~25%之间 | B. | 在25~50%之间 | C. | 在50~75%之间 | D. | 在75~100%之间 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{9}{4}$,+∞) | B. | [-$\frac{9}{4}$,+∞) | C. | (-$\frac{9}{4}$,-2] | D. | (-$\frac{9}{4}$,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com