
| A. | (-$\frac{9}{4}$,+∞) | B. | [-$\frac{9}{4}$,+∞) | C. | (-$\frac{9}{4}$,-2] | D. | (-$\frac{9}{4}$,-2) |
分析 由“和谐函数”的定义,及函数$f(x)=k+\sqrt{x+2}$的解析式,我们可得函数满足条件(1),即在定义域D内是单调函数,若满足条件(2)则$f(x)=k+\sqrt{x+2}$=x在区间[-2,+∞)上有两个根,利用换元法,可将条件转化为t2-t-(2+k)=0有两个非负根,结合二次方程根与系数的关系,可得关于k的不等式组,进而求出k的范围.
解答 解:∵$f(x)=k+\sqrt{x+2}$在定义域D=[-2,+∞)上为增函数
故满足条件(1)
若存在[a,b]⊆D使f(x)在x∈[a,b]值域为[a,b],
则$f(x)=k+\sqrt{x+2}$=x在区间[-2,+∞)上有两个根
令t=$\sqrt{x+2}$(t≥0)
则原方程可化为t2-t-(2+k)=0有两个非负根
即$\left\{\begin{array}{l}△=1+4(2+k)>0\\ 2+k≤0\end{array}\right.$
解得-$\frac{9}{4}$<k≤-2
故k的范围是$(-\frac{9}{4},-2]$
故选:C.
点评 本题考查的知识点是单调性的性质,其中正确理解新定义“闭函数”中的两个条件的意义,是解答本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $(0,\sqrt{3})$ | B. | $(-\sqrt{3},0)$ | C. | $(-\sqrt{3},\sqrt{3}]$ | D. | $(-\sqrt{3},\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 等腰三角形 | ||
| C. | 直角三角形 | D. | 等腰或直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
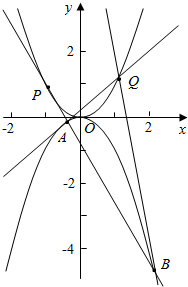 如图,过抛物线${C_1}:{x^2}=2py$上的一点Q与抛物线${C_2}:{x^2}=-2py$相切于A,B两点.若抛物线${C_1}:{x^2}=2py$的焦点F1到抛物线${C_2}:{x^2}=-2py$的焦点F2的距离为$\frac{1}{2}$
如图,过抛物线${C_1}:{x^2}=2py$上的一点Q与抛物线${C_2}:{x^2}=-2py$相切于A,B两点.若抛物线${C_1}:{x^2}=2py$的焦点F1到抛物线${C_2}:{x^2}=-2py$的焦点F2的距离为$\frac{1}{2}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com