
分析 换元可得原式=$\frac{1}{2}$(1+$\frac{1-t}{{t}^{2}+3t}$),m≤0,由基本不等式和不等式的性质分类讨论综合可得.
解答 解:令1+2x2=t,则t≥1,且x2=$\frac{1}{2}$(t-1)
换元可得y=$\frac{\frac{(t+1)^{2}}{4}}{t(\frac{t+3}{2})}$=$\frac{1}{2}$•$\frac{{t}^{2}+2t+1}{{t}^{2}+3t}$
=$\frac{1}{2}$•$\frac{{t}^{2}+3t-t+1}{{t}^{2}+3t}$=$\frac{1}{2}$(1+$\frac{1-t}{{t}^{2}+3t}$),
再令1-t=m则m≤0且t=1-m,
当m=0时,$\frac{1}{2}$(1+$\frac{1-t}{{t}^{2}+3t}$)=$\frac{1}{2}$(1+$\frac{m}{{m}^{2}-5m+4}$)=$\frac{1}{2}$;
当m≤0时,$\frac{1}{2}$(1+$\frac{1-t}{{t}^{2}+3t}$)=$\frac{1}{2}$(1+$\frac{m}{{m}^{2}-5m+4}$)
=$\frac{1}{2}$(1+$\frac{1}{m+\frac{4}{m}-5}$),
∵m<0,∴m+$\frac{4}{m}$=-(-m+$\frac{4}{-m}$)≤-2$\sqrt{-m•\frac{4}{-m}}$=-4,
当且仅当-m=$\frac{4}{-m}$即m=-2时取等号,
∴m+$\frac{4}{m}$-5≤=-4-5=-9,
∴-$\frac{1}{9}$≤$\frac{1}{m+\frac{4}{m}-5}$)<0,
∴$\frac{8}{9}$≤1+$\frac{1}{m+\frac{4}{m}-5}$<1,
∴$\frac{4}{9}$≤$\frac{1}{2}$(1+$\frac{25}{m+\frac{16}{m}-17}$)<$\frac{1}{2}$;
综合可得函数的值为[$\frac{4}{9}$,$\frac{1}{2}$]
点评 本题考查函数值域的求解,涉及换元法和基本不等式求最值以及不等式的性质,属中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
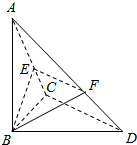 已知△ABC中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别为AC,AD上的动点,且AE:AC=AF:AD=k,k∈(0,1).
已知△ABC中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别为AC,AD上的动点,且AE:AC=AF:AD=k,k∈(0,1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面是边长为a的菱形,平面PCD⊥平面ABCD,PC=a,PD=$\sqrt{2}$a,E为PA的中点,求证:平面EDB⊥平面ABCD.
如图,四棱锥P-ABCD的底面是边长为a的菱形,平面PCD⊥平面ABCD,PC=a,PD=$\sqrt{2}$a,E为PA的中点,求证:平面EDB⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | $±\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2\sqrt{3}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
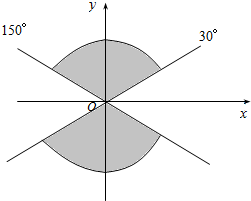 已知角α的终边在图中阴影部分所表示的范围内(不包括边界),则α的取值范围为{α|k•180°+30°<α<k•180°+150°,k∈Z}.
已知角α的终边在图中阴影部分所表示的范围内(不包括边界),则α的取值范围为{α|k•180°+30°<α<k•180°+150°,k∈Z}.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com