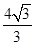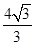分析:本题考查的知识点是由三视图求面积、体积,是近年来高考的必考内容,由主视图、左视图所对应的三角形皆为边长为2的正三角形,俯视图对应的四边形为正方形,我们易得该几何体为底面边长为2,高为
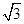
的正四棱锥,将底面边长及高代入棱锥体积公式,即可得到这个几何体的体积.
解答:解:∵主视图、左视图所对应的三角形皆为边长为2的正三角形,
俯视图对应的四边形为正方形,
∴几何体为底面边长为2,高为
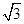
的正四棱锥
则V=
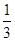
?2
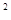
?
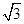
=
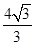
故答案为:
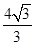
点评:根据三视图判断空间几何体的形状,进而求几何的表(侧/底)面积或体积,是高考必考内容,处理的关键是准确判断空间几何体的形状,一般规律是这样的:如果三视图均为三角形,则该几何体必为三棱锥;如果三视图中有两个三角形和一个多边形,则该几何体为N棱锥(N值由另外一个视图的边数确定);如果三视图中有两个为矩形和一个多边形,则该几何体为N棱柱(N值由另外一个视图的边数确定);如果三视图中有两个为梯形和一个多边形,则该几何体为N棱柱(N值由另外一个视图的边数确定);如果三视图中有两个三角形和一个圆,则几何体为圆锥.如果三视图中有两个矩形和一个圆,则几何体为圆柱.如果三视图中有两个梯形和一个圆,则几何体为圆台.


 B .
B .  C.
C.  D .
D . 
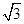 的正四棱锥,将底面边长及高代入棱锥体积公式,即可得到这个几何体的体积.
的正四棱锥,将底面边长及高代入棱锥体积公式,即可得到这个几何体的体积.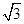 的正四棱锥
的正四棱锥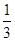 ?2
?2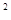 ?
?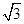 =
=