
(08年四川卷理)设椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,离心率
,离心率![]() ,右准线
,右准线![]() 上的两动点
上的两动点![]() 、
、![]() ,且
,且![]() .
.
(Ⅰ)若![]() ,求
,求![]() 、
、![]() 的值;
的值;
(Ⅱ)当![]() 最小时,求证
最小时,求证![]() 与
与![]() 共线.
共线.

解析:数列和解几位列倒数第三和第二,意料之中.开始挤牙膏吧.
(Ⅰ)由已知,![]() ,
,![]() .由
.由![]() ,
,![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() :
:![]() ,
,![]() ,
,![]() .
.
延长![]() 交
交![]() 于
于![]() ,记右准线
,记右准线![]() 交
交![]() 轴于
轴于![]() .
.
∵![]() ,∴
,∴![]() .
.![]()
由平几知识易证![]() ≌
≌![]()
∴![]() ,
,![]()
即![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
(Ⅰ)另解:∵![]() ,∴
,∴![]() ,
,![]() .
.
又![]()
联立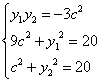 ,消去
,消去![]() 、
、![]() 得:
得:![]() ,
,
整理得:![]() ,
,![]() .解得
.解得![]() .但解此方程组要考倒不少人.
.但解此方程组要考倒不少人.
(Ⅱ)∵![]() ,∴
,∴![]() .
.
![]() .
.
当且仅当![]() 或
或![]() 时,取等号.此时
时,取等号.此时![]() 取最小值
取最小值![]() .
.
此时![]() .
.
∴![]() 与
与![]() 共线.
共线.
(Ⅱ)另解:∵![]() ,∴
,∴![]() ,
,![]() .
.
设![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
由![]() ,由
,由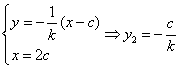
![]() .当且仅当
.当且仅当![]() 即
即![]() ,
,![]() 时取等号.
时取等号.
即当![]() 最小时,
最小时,![]() ,
,
此时![]() .
.
∴![]() 与
与![]() 共线.
共线.
点评:本题第一问又用到了平面几何.看来,与平面几何有联系的难题真是四川风格啊.注意平面几何可与三角向量解几沾边,应加强对含平面几何背景的试题的研究.本题好得好,出得活,出得妙!均值定理,放缩技巧,永恒的考点.


科目:高中数学 来源: 题型:
(08年四川卷理)设进入某商场的每一位顾客购买甲商品的概率0.5,购买乙商品的概率为0.6,且顾客购买甲商品与购买乙商品相互独立,每位顾客间购买商品也相互独立.
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(Ⅲ)设![]() 是进入商场的3位顾客至少购买甲、乙商品中一种的人数,求
是进入商场的3位顾客至少购买甲、乙商品中一种的人数,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com