已知数列{an}中,a1=1,前n项和sn满足sn+1-sn=2n+1(n∈N*).
(Ⅰ)求数列{an}的通项公式及前n项和sn;
(Ⅱ)若S1、t(S3+S4)(t>0)的等差中项不大于它们的等比中项,求t的值.
解:(Ⅰ)当n≥2时,a
n=S
n-S
n-1=2(n-1)+1=2n-1
因为a
1=1也满足上式,所以数列{a
n}的通项公式:a
n=2n-1(n∈N
*)
又因为a
n+1-a
n=2(n+1)-1-(2n-1)=2为定值,所以{a
n}为等差数列
所以数列{a
n}前n项和:

(n∈N
*)
(Ⅱ)由(Ⅰ)可得 S
1=1,t(S
3+S
4)=25t
又由题意,得
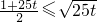
整理,得
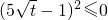
,所以

,则
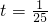
.
分析:(Ⅰ)分析题意可知是由s
n求a
n故需利用a
n与s
n的关系:当n≥2时,a
n=s
n-s
n-1来求解同时需验证a
1=1是否也满足上式.当a
n求出后分析它的特征然后决定采用什么方法求前n项和.
(Ⅱ)可由(1)求出S
1,t(S
3+S
4)然后利用S
1、t(S
3+S
4)(t>0)的等差中项不大于它们的等比中项列出关于t 的关系式再求解即可.
点评:本题主要考查了利用数列前n项和s
n的递推关系式求数列的通项.解题的关键是要利用a
n与s
n的关系:当n≥2时,a
n=s
n-s
n-1求a
n同时需验证a
1=1是否也符合而求出a
n后下面的问题就迎刃而解了.本题容易遗漏的是对n=1时a
1=1是否也符合的验证!

 (n∈N*)
(n∈N*)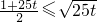
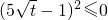 ,所以
,所以 ,则
,则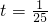 .
.
